早教吧作业答案频道 -->数学-->
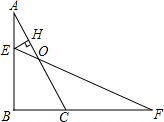
如图,在直角三角形ABC中,点E在线段AB上,过点E作EH⊥AC交AC于点H,点F在BC的延长线上,连结EF交AC于点O.若AB=2,BC=1,且CFAE=2,则OEOF=,OH=.
题目详情
如图,在直角三角形ABC中,点E在线段AB上,过点E作EH⊥AC交AC于点H,点F在BC的延长线上,连结EF交AC于点O.若AB=2,BC=1,且
=2,则
=___,OH=___.
| CF |
| AE |
| OE |
| OF |

▼优质解答
答案和解析
过点E作ED∥BF.
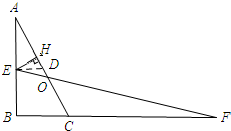
∵ED∥BF.
∴△AED∽△ABC,△EDO∽△FCO.
∴
=
=
,
=
.
∴ED=
AE.
又∵CF=2AE,
∴CF=4ED.
∴
=
=
.
∵∠EDH=∠AED,∠EHD=∠AED=90°,
∴△EHD∽△AED.
∵∠A=∠A,∠AHE=∠AED,
∴△AED∽△AEH.
∴△DHE∽△AEH.
∴AH=2EH=4DH.
∵△EDO∽△FCO,
∴
=
=
.
∴OC=4OD.
∴AH+OC=4DH+4OD=4HO.
∴AC=5HO.
在Rt△ABC中,AC=
=
=
.
∴OH=
=
.
故答案为:
;
.

∵ED∥BF.
∴△AED∽△ABC,△EDO∽△FCO.
∴
| ED |
| AE |
| BC |
| AB |
| 1 |
| 2 |
| OE |
| OF |
| ED |
| CF |
∴ED=
| 1 |
| 2 |
又∵CF=2AE,
∴CF=4ED.
∴
| OE |
| OF |
| DE |
| 4ED |
| 1 |
| 4 |
∵∠EDH=∠AED,∠EHD=∠AED=90°,
∴△EHD∽△AED.
∵∠A=∠A,∠AHE=∠AED,
∴△AED∽△AEH.
∴△DHE∽△AEH.
∴AH=2EH=4DH.
∵△EDO∽△FCO,
∴
| OD |
| OC |
| OE |
| OF |
| 1 |
| 4 |
∴OC=4OD.
∴AH+OC=4DH+4OD=4HO.
∴AC=5HO.
在Rt△ABC中,AC=
| AB2+BC2 |
| 22+12 |
| 5 |
∴OH=
| AC |
| 5 |
| ||
| 5 |
故答案为:
| 1 |
| 4 |
| ||
| 5 |
看了 如图,在直角三角形ABC中,...的网友还看了以下:
已知,如图,矩形ABCD中,AD=a,DC=b,在AB上找一点E,a,b满足什么要求时,存在点E与 2020-04-09 …
如图,三角形abc,内部的一点d,关于边ab ac,的对称点分别是点e f.一.判断三角形a e如 2020-05-13 …
在三角形ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果在AB上找一点E,使三角形AD 2020-05-15 …
P是三角形ABC平面外一点,D、E是三角形PAB和PBC重心P是三角形ABC平面外一点,D、E是三 2020-05-22 …
已知三角形ABC中,AB=AC,D,E在三角形ABC中,AB=AC,点D,E是BC边上的点,将三角 2020-07-21 …
三角形abc的内角abc和外角ac的角平分线交于点e,be交ac于f,过点e做eg平行于bd交a三 2020-07-31 …
几道相似、比例的数学1、在直角三角形ABC中,角A=90度,角B=30度,D在AB边上,E在AC边 2020-08-03 …
数学向量1,A,B,C,D为平面上4个互异点,且满足(向量DB+DC-2DA)点乘(AB-AC)=0 2020-11-02 …
三道分解因式填空题急用1/4a^2+ab+mb^2,是个完全平方式,则m=()若(p-q)^2-(q 2020-12-05 …
在真空中三个等量点电荷固定在正三角形的三个顶点,如图所示,c、d、e为三角形三个边的中点,下列判断正 2020-12-24 …