若点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，则△ABC的面积为（）A.2+3B.233C.2+3或2-3D.4+23或2-3

Question

若点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，则△ABC的面积为（　　）

A. 2+

√(3)

B.

(2√(3))/(3)

C. 2+

√(3)或2-√(3)

D. 4+2

√(3)或2-√(3)

Answer 1

由题意可得，如右图所示，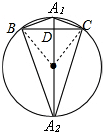
存在两种情况，
当△ABC为△A₁BC时，连接OB、OC，
∵点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，OB=OC，
∴△OBC为等边三角形，OB=OC=BC=2，OA₁⊥BC于点D，
∴CD=1，OD=√(22-12)=√(3)，
∴S△A1BC=(BC•A1D)/(2)=(2×(2-√(3)))/(2)=2-√(3)，
当△ABC为△A₂BC时，连接OB、OC，
∵点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，OB=OC，
∴△OBC为等边三角形，OB=OC=BC=2，OA₁⊥BC于点D，
∴CD=1，OD=√(22-12)=√(3)，
∴S_△A2BC=(BC•DA2)/(2)=(2×(2+√(3)))/(2)=2+√(3)，
由上可得，△ABC的面积为2-√(3)或2+

作业帮用户 2017-05-12

问题解析

根据题意可以画出相应的图形，然后根据不同情况，求出相应的边的长度，从而可以求出不同情况下△ABC的面积，本题得以解决．

名师点评

本题考点：

三角形的外接圆与外心 等腰三角形的性质

考点点评：

本题考查三角形的外接圆和外心，等腰三角形的性质，解题的关键是明确题意，找出所求问题需要的条件，利用分类讨论的数学思想解答问题．

扫描下载二维码

©2018 作业帮 联系方式：[e-mail]  作业帮协议