早教吧作业答案频道 -->数学-->
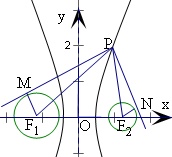
过双曲线x2-y215=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x-4)2+y2=1作切线,切点分别为M,N,则|PM|2-|PN|2的最小值为.
题目详情
过双曲线x2-
=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x-4)2+y2=1作切线,切点分别为M,N,则|PM|2-|PN|2的最小值为___.
| y2 |
| 15 |
▼优质解答
答案和解析
 圆C1:(x+4)2+y2=4的圆心为(-4,0),半径为r1=2;
圆C1:(x+4)2+y2=4的圆心为(-4,0),半径为r1=2;
圆C2:(x-4)2+y2=1的圆心为(4,0),半径为r2=1,
设双曲线x2-
=1的左右焦点为F1(-4,0),F2(4,0),
连接PF1,PF2,F1M,F2N,可得
|PM|2-|PN|2=(|PF1|2-r12)-(|PF2|2-r22)
=(|PF1|2-4)-(|PF2|2-1)
═|PF1|2-|PF2|2-3=(|PF1|-|PF2|)(|PF1|+|PF2|)-3
=2a(|PF1|+|PF2|-3=2(|PF1|+|PF2|)-3≥2•2c-3=2•8-3=13.
当且仅当P为右顶点时,取得等号,即最小值13.
故答案为:13.
 圆C1:(x+4)2+y2=4的圆心为(-4,0),半径为r1=2;
圆C1:(x+4)2+y2=4的圆心为(-4,0),半径为r1=2;圆C2:(x-4)2+y2=1的圆心为(4,0),半径为r2=1,
设双曲线x2-
| y2 |
| 15 |
连接PF1,PF2,F1M,F2N,可得
|PM|2-|PN|2=(|PF1|2-r12)-(|PF2|2-r22)
=(|PF1|2-4)-(|PF2|2-1)
═|PF1|2-|PF2|2-3=(|PF1|-|PF2|)(|PF1|+|PF2|)-3
=2a(|PF1|+|PF2|-3=2(|PF1|+|PF2|)-3≥2•2c-3=2•8-3=13.
当且仅当P为右顶点时,取得等号,即最小值13.
故答案为:13.
看了 过双曲线x2-y215=1的...的网友还看了以下:
1.直线√3х-3y+1=0的斜角为?2.椭圆的长轴长是短轴长的2倍,则椭圆的离心率为?3.双曲线 2020-05-23 …
已知椭圆的中心为坐标原点O,椭圆短轴长为2,动点M(2,t)(t>0)在椭圆的准线上.(Ⅰ)求椭圆 2020-06-21 …
已知椭圆的中心为坐标原点O,椭圆短半轴长为1,动点M(2,t)(t>0)在直线x=a2c(a为长半 2020-06-21 …
已知椭圆x^2/a^2+y^2/b^2=1(a>b>0)的长轴长和短轴长之差是2√2-2,且右焦点 2020-06-21 …
已知半径为2,圆心在直线y=-x+2上的圆C.(Ⅰ)当圆C经过点A(2,2)且与y轴相切时,求圆C 2020-06-30 …
弧,玄,圆心角题(1)圆O中,玄AB=3,圆心角AOB=120,则圆O的半径是?(2)A,B,C, 2020-07-02 …
.(本题满分14分)已知椭圆的中心为坐标原点O,焦点在X轴上,椭圆短半轴长为1,动点在直线上。(1 2020-07-15 …
已知以点C(a,b)为圆心,半径为r的圆的标准方程为(x-a)2+(y-b)2=r2.例如:以A( 2020-07-16 …
两角相等,已知圆O的半径为2,以圆O的弦AB为直径作圆M,点C是圆O优弧AB上的一个动点(不与点A 2020-07-31 …
已知椭圆C的长轴长是短轴长只差是2根号2-2,且右焦点F到此椭圆的一个短轴端点的的距离为√2,点C 2020-07-31 …