早教吧作业答案频道 -->数学-->
如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.(1)如图2、图3,当∠CDF=0°或60°
题目详情
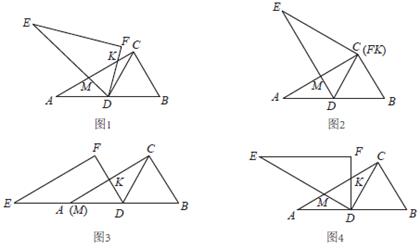
如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.
(1)如图2、图3,当∠CDF=0°或60°时,AM+CK___MK(填“>”,“<”或“=”),你的依据是___;
(2)如图4,当∠CDF=30°时,AM+CK___MK(填“>”或“<”);
(3)猜想:如图1,当0°<∠CDF<60°时,AM+CK___MK,试证明你的猜想.
(1)如图2、图3,当∠CDF=0°或60°时,AM+CK___MK(填“>”,“<”或“=”),你的依据是___;
(2)如图4,当∠CDF=30°时,AM+CK___MK(填“>”或“<”);
(3)猜想:如图1,当0°<∠CDF<60°时,AM+CK___MK,试证明你的猜想.

▼优质解答
答案和解析
(1)在Rt△ABC中,D是AB的中点,
∴AD=BD=CD=
AB,∠B=∠BDC=60°
又∵∠A=30°,
∴∠ACD=60°-30°=30°,
又∵∠CDE=60°,或∠CDF=60°时,
∴∠CKD=90°,
∴在△CDA中,AM(K)=CM(K),即AM(K)=KM(C)(等腰三角形底边上的垂线与中线重合),
∵CK=0,或AM=0,
∴AM+CK=MK;
(2)由(1),得∠ACD=30°,∠CDB=60°,
又∵∠A=30°,∠CDF=30°,∠EDF=60°,
∴∠ADM=30°,
∴AM=MD,CK=KD,
∴AM+CK=MD+KD,
∴在△MKD中,AM+CK>MK,
(3)AM+CK>MK,
证明:作点A关于ED的对称点G,连接GK,GM,GD.
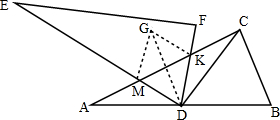
∵点G是点A关于直线DE的对称点
∴AD=GD,GM=AM,∠GDM=∠ADM,
∵Rt△ABC 中,D是AB的中点,
∴AD=CD=GD.
∵∠A=∠E=30°,
∴∠CDA=120°,∠EDF=60°,
∴∠GDM+∠GDK=60°,∠ADM+∠CDK=60°,
∴∠GDK=∠CDK,
在△GDK和△CDK中,
∵
,
∴△GDK≌△CDK(SAS),
∴GK=CK,
∵GM+GK>MK,
∴AM+CK>MK.
∴AD=BD=CD=
| 1 |
| 2 |
又∵∠A=30°,
∴∠ACD=60°-30°=30°,
又∵∠CDE=60°,或∠CDF=60°时,
∴∠CKD=90°,
∴在△CDA中,AM(K)=CM(K),即AM(K)=KM(C)(等腰三角形底边上的垂线与中线重合),
∵CK=0,或AM=0,
∴AM+CK=MK;
(2)由(1),得∠ACD=30°,∠CDB=60°,
又∵∠A=30°,∠CDF=30°,∠EDF=60°,
∴∠ADM=30°,
∴AM=MD,CK=KD,
∴AM+CK=MD+KD,
∴在△MKD中,AM+CK>MK,
(3)AM+CK>MK,
证明:作点A关于ED的对称点G,连接GK,GM,GD.

∵点G是点A关于直线DE的对称点
∴AD=GD,GM=AM,∠GDM=∠ADM,
∵Rt△ABC 中,D是AB的中点,
∴AD=CD=GD.
∵∠A=∠E=30°,
∴∠CDA=120°,∠EDF=60°,
∴∠GDM+∠GDK=60°,∠ADM+∠CDK=60°,
∴∠GDK=∠CDK,
在△GDK和△CDK中,
∵
|
∴△GDK≌△CDK(SAS),
∴GK=CK,
∵GM+GK>MK,
∴AM+CK>MK.
看了 如图1,有两个全等的直角三角...的网友还看了以下:
计算√17√9-√1若a的二次方=4b的二次方=9,且a>0,b<0,试求a+b的值16的算术平方 2020-04-11 …
用适当的方法表示下列集合(1)大于-3且小于10的所有正偶数构成的集合(2)大于0.9且不大于6的 2020-04-11 …
2个1/3等于几个1/9?一个分数的分母扩大2倍,分子缩小2倍,这个分数的值倍.若3/4小于x/3 2020-04-27 …
排列组合问题某城实行五位车牌号,其中至少含有一个9且各数之和为9的倍数的号码有几个?首位不为0 2020-05-17 …
自旋怎么产生?且自旋为1/2的模型是怎么样的?要以生活中的实例加以说明! 2020-05-17 …
已知丨x丨=4,丨y丨=3,且x小于y,则x-y=几已知丨x丨=4,y的平方=9,且丨x-y丨=y 2020-06-16 …
如图,在平面直角坐标系中,A点坐标为(3,0),线段OA绕原点O每次按逆时针方向旋转60°,并且每 2020-07-09 …
如图所示为四旋翼飞行器,是一种有4个螺旋桨且螺旋桨呈十字形交叉,能够垂直起降的小型遥控飞行器,通常 2020-07-15 …
若(x+2+m)^9=a0+a1(x+1)^2+.+a9(x+1)^9,且(a0+a2+....+a 2020-10-31 …
求a=b=c的值求AB:BM的值.(1)若a:b:c=3:5:7,且3a+2b-4c=9,且3a+2 2020-12-02 …