早教吧作业答案频道 -->数学-->
已知三棱锥P-ABC的各顶点都在同一球的面上,且PA⊥平面ABC,若球O的体积为205π3(球的体积公式为4π3R3,其中R为球的半径),AB=2,AC=1,∠BAC=60°,则三棱锥P-ABC的体积为()A.33B.233C.
题目详情
已知三棱锥P-ABC的各顶点都在同一球的面上,且PA⊥平面ABC,若球O的体积为
(球的体积公式为20
π5 3
R3,其中R为球的半径),AB=2,AC=1,∠BAC=60°,则三棱锥P-ABC的体积为( )4π 3
A. 3 3
B. 2 3 3
C. 3
D. 4 3 3
▼优质解答
答案和解析
如图所示,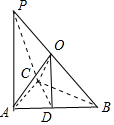 在△ABC中,AB=2,AC=1,∠BAC=60°,则BC2=22+12-2×1×2×cos60°=3,
在△ABC中,AB=2,AC=1,∠BAC=60°,则BC2=22+12-2×1×2×cos60°=3,
解得BC=
,∴12+(
)2=22.
∴∠ACB=90°.
取AB的中点D,则球心O满足OD⊥平面ABC.
又PA⊥平面ABC,∴三棱锥P-ABC的外接球的球心O为PB的中点.
∴OD=
PA.
由球的体积计算公式可得:
R3=
,解得R=
.
∴OD=
=2.
∴PA=4
∴三棱锥P-ABC的体积V=
×S△ABC×PA=
×
×1×
×4=
.
故选:B.
 在△ABC中,AB=2,AC=1,∠BAC=60°,则BC2=22+12-2×1×2×cos60°=3,
在△ABC中,AB=2,AC=1,∠BAC=60°,则BC2=22+12-2×1×2×cos60°=3,解得BC=
| 3 |
| 3 |
∴∠ACB=90°.
取AB的中点D,则球心O满足OD⊥平面ABC.
又PA⊥平面ABC,∴三棱锥P-ABC的外接球的球心O为PB的中点.
∴OD=
| 1 |
| 2 |
由球的体积计算公式可得:
| 4π |
| 3 |
20
| ||
| 3 |
| 5 |
∴OD=
| R2-AD2 |
∴PA=4
∴三棱锥P-ABC的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
故选:B.
看了 已知三棱锥P-ABC的各顶点...的网友还看了以下:
下列格式中能用完全平方公式分解因式的是?A、(x+y)(y-x)-4xyB、a^2-2ab+4b^2 2020-03-31 …
ab=-1,a=b=2,则式子b/a+a/b= 2020-04-05 …
若ab=-1,a+b=2,则式子b/a+a/b=() 2020-04-05 …
一.下列多项式不能用平方差公式分解因式的是( )A,4分之一x的平方y的平方-4 B,4-0.25 2020-05-14 …
已知a³+b³=27,a²b-ab²=-6,求代数式(b³-a³)+(a²b-3ab²)-2(已知 2020-05-16 …
向量a与b共线有个公式是b=λa,如果它们不共线,这个公式应该也成立啊,λ是实数, 2020-05-16 …
谁能告诉我在不知度数的情况下计算扇形面积的公式,在知道扇形周边长的情况下还有一道数学题.已知a,b 2020-05-17 …
不要光写答案,怎么解答的过程也写清楚,这样我才采纳.当a时,多项式(3-2a)x^2+(b-1)x 2020-05-17 …
已知数a,b,c的大小关系如图所示:则下列各式:①b+a+(-c)>0;②(-a)-b+c>0;③ 2020-06-12 …
有一道题目“当a=2,b=-2时,求多项式3a³b³-½a²b+b-(4a³b³-¼a²b-b²) 2020-06-12 …