早教吧作业答案频道 -->数学-->
在三棱柱ABC-A1B1C1中,△ABC是正三角形,且A1A=AB,顶点A1在底面ABC上的射影是△ABC的中心.(1)求证:AA1⊥BC;(2)求直线A1B与平面BCC1B1所成角的大小.
题目详情
在三棱柱ABC-A1B1C1中,△ABC是正三角形,且A1A=AB,顶点A1在底面ABC上的射影是△ABC的中心.
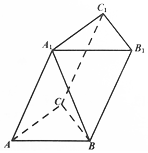
(1)求证:AA1⊥BC;
(2)求直线A1B与平面BCC1B1所成角的大小.

(1)求证:AA1⊥BC;
(2)求直线A1B与平面BCC1B1所成角的大小.
▼优质解答
答案和解析
(1)证明:如图,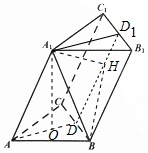
∵A1O⊥底面ABC,∴A1O⊥BC,
∵△ABC为正三角形,O为底面三角形的中心,
连接AO交BC于D,则AD⊥BC,
又AD∩A1D=O,∴BC⊥平面A1AD,
则AA1⊥BC;
(2) 取B1C1的中点D1,连接A1D1,DD1,
由(1)知,BC⊥平面ADD1A1,
∴平面ADD1A1⊥平面BB1C1C,且平面ADD1A1∩平面BB1C1C=DD1,
过A1作A1H⊥DD1,垂足为H,连接BH,
则∠A1BH为直线A1B与平面BCC1B1所成角.
设A1A=AB=2a,可得A1O=
a,
由AD•A1O=AA1•A1H,得A1H=
=
=
a.
在Rt△A1HB中,sin∠A1BH=
=
.
∴直线A1B与平面BCC1B1所成角为45°.

∵A1O⊥底面ABC,∴A1O⊥BC,
∵△ABC为正三角形,O为底面三角形的中心,
连接AO交BC于D,则AD⊥BC,
又AD∩A1D=O,∴BC⊥平面A1AD,
则AA1⊥BC;
(2) 取B1C1的中点D1,连接A1D1,DD1,
由(1)知,BC⊥平面ADD1A1,
∴平面ADD1A1⊥平面BB1C1C,且平面ADD1A1∩平面BB1C1C=DD1,
过A1作A1H⊥DD1,垂足为H,连接BH,
则∠A1BH为直线A1B与平面BCC1B1所成角.
设A1A=AB=2a,可得A1O=
2
| ||
| 3 |
由AD•A1O=AA1•A1H,得A1H=
| AD•A1O |
| A1A |
| ||||||
| 2a |
| 2 |
在Rt△A1HB中,sin∠A1BH=
| ||
| 2a |
| ||
| 2 |
∴直线A1B与平面BCC1B1所成角为45°.
看了 在三棱柱ABC-A1B1C1...的网友还看了以下:
把边长为4的等边三角形ABC置于直角坐标系中,使得顶点B在原点,顶点C在x轴上,若点C把边长为4的 2020-05-16 …
一个人在某建筑物AB的顶部A测得一烟囱CD的顶端C的仰角为45度,测得顶端C在湖中的倒影C`的俯角 2020-05-17 …
在比水面高2m的A地观测河对岸有一棵树BC的顶部B的仰角为30度它在水中的倒影B'C顶部B'的俯角 2020-05-17 …
建筑物外,有柱和顶盖的走廊,其建筑面积按( )计算。A.柱外围水平面积B.顶盖的水平投影面积C.顶 2020-05-21 …
在众多的逻辑名题中,影响最广泛的,恐怕要数"猜帽问题"了.下面,举一个例子来说明这类问题的概貌.有 2020-06-22 …
如图所示的四种现象中,属于光的折射的是()A.镜中的像B.丹顶鹤的倒影C.变扁的太阳D.灯下的影子 2020-06-27 …
下图中阴影部分表示夜半球,非阴影部分表示昼半球,分析回答下列问题。(8分)(1)日晷的轨迹就是旗杆 2020-06-27 …
无向图中一个顶点的度是指图中A.通过该顶点的简单路径数B.通过该顶点的回路数C.与该顶点相铃的顶点 2020-06-30 …
下列说法正确的是()A.圆台是直角梯形绕其一边旋转而成的旋转体B.棱台的上下底面一定相似,但侧棱长 2020-07-25 …
小明在晚上由路灯A走向路灯B,当他走到P处时,发现身后影子顶部正好触到路灯A底部,当他向前再步行12 2020-11-25 …