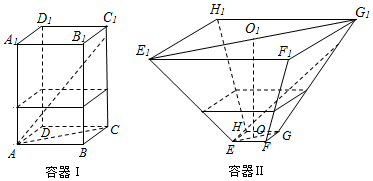
如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为107cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ

Question

如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10√(7)cm，容器Ⅱ的两底面对角线EG，E₁G₁的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm．现有一根玻璃棒l，其长度为40cm．（容器厚度、玻璃棒粗细均忽略不计）
（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC₁上，求l没入水中部分的长度；
（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG₁上，求l没入水中部分的长度．

Answer 1

（1）设玻璃棒在CC₁上的点为M，玻璃棒与水面的交点为N，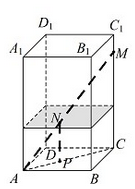
在平面ACM中，过N作NP∥MC，交AC于点P，
∵ABCD-A₁B₁C₁D₁为正四棱柱，∴CC₁⊥平面ABCD，
又∵AC⊂平面ABCD，∴CC₁⊥AC，∴NP⊥AC，
∴NP=12cm，且AM²=AC²+MC²，解得MC=30cm，
∵NP∥MC，∴△ANP∽△AMC，
∴(AN)/(AM)=(NP)/(MC)，(AN)/(40)=(12)/(30)，得AN=16cm．
∴玻璃棒l没入水中部分的长度为16cm．
（2）设玻璃棒在GG₁上的点为M，玻璃棒与水面的交点为N，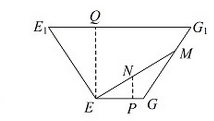
在平面E₁EGG₁中，过点N作NP⊥EG，交EG于点P，
过点E作EQ⊥E₁G₁，交E₁G₁于点Q，
∵EFGH-E₁F₁G₁H₁为正四棱台，∴EE₁=GG₁，EG∥E₁G₁，
EG≠E₁G₁，
∴EE₁G₁G为等腰梯形，画出平面E₁EGG₁的平面图，
∵E₁G₁=62cm，EG=14cm，EQ=32cm，NP=12cm，
∴E₁Q=24cm，
由勾股定理得：E₁E=40cm，
∴sin∠EE₁G₁=(4)/(5)，sin∠EGM=sin∠EE₁G₁=(4)/(5)，cos∠EGM=-(3)/(5)，
根据正弦定理得：(EM)/(sin∠EGM)=(EG)/(sin∠EMG)，∴sin∠EMG=(7)/(25)，cos∠EMG=(24)/(25)，
∴sin∠GEM=sin（∠EGM+∠EMG）=sin∠EGMcos∠EMG+cos∠EGMsin∠EMG=(3)/(5)，
∴EN=(NP)/(sin∠GEM)=(12)/((3)/(5))=20cm．
∴玻璃棒l没入水中部分的长度为20cm．