早教吧作业答案频道 -->数学-->
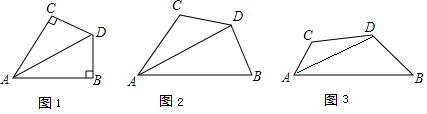
如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.(1)如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.(2)如图3,四边形ABCD中,∠B=60°,∠C=120°,DB=DC=2,则AB-AC=?
题目详情
如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.
(1)如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
(2)如图3,四边形ABCD中,∠B=60°,∠C=120°,DB=DC=2,则AB-AC=?
(1)如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
(2)如图3,四边形ABCD中,∠B=60°,∠C=120°,DB=DC=2,则AB-AC=?

▼优质解答
答案和解析
(1)证明:如图②中,DE⊥AB于E,DF⊥AC于F,
∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,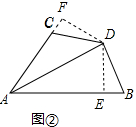
,
∴△DFC≌△DEB,
∴DC=DB.
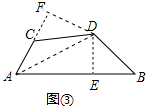
(2) 如图③连接AD、DE⊥AB于E,DF⊥AC于F,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,
,
∴△DFC≌△DEB,
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,
,
∴△ADF≌△ADE,
∴AF=AE,
∴AB-AC=(AE+BE)-(AF-CF)=2BE,
在Rt△DEB中,∵∠DEB=90°,∠B=∠EDB=60°,BD=2,
∴BE=1,
∴AB-AC=2.
∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,

|
∴△DFC≌△DEB,
∴DC=DB.
(2) 如图③连接AD、DE⊥AB于E,DF⊥AC于F,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,
|

∴△DFC≌△DEB,
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,
|
∴△ADF≌△ADE,
∴AF=AE,
∴AB-AC=(AE+BE)-(AF-CF)=2BE,
在Rt△DEB中,∵∠DEB=90°,∠B=∠EDB=60°,BD=2,
∴BE=1,
∴AB-AC=2.
看了 如图1,AD平分∠BAC,∠...的网友还看了以下:
根据反应:①2C-+A2=2A-+C2;②2B-+D2=2D-+B2;③2A-+B2=2B-+A2 2020-07-09 …
下列漫画中,符合共同富裕原则要求的是A.B.C.D. 2020-07-15 …
真正的友谊表现为()①不含嫉妒之心,没有狭隘之意②投其所好,获取利益③真诚为朋友的成功祝福④相互迁 2020-07-16 …
元朝时期,由中央直辖的省份是()①河北②河南③山西④山东A.①②④B.①③④C.②③④D.①②③④ 2020-07-28 …
向量两题1.设三角形ABC的外心为O,垂心为H.求证向量OH=OA+OB=OC2.在三角形ABC中 2020-07-30 …
图为某地区港口分布示意图。完成b.c.d三港口封冻期由长到短排序正确的是A.c>d.>bB.d>c> 2020-11-04 …
在第二国际内部既属于左派代表又属于德国人的是①伯恩施坦②普列汉诺夫③卡尔卜克内西④罗莎·卢森堡[]A 2020-11-08 …
一、单选题(多选、错选均不得分;每题3分)1.函数:的定义域是:()A.B.C.D.2.若函数可导一 2020-12-13 …
该半岛人口和大城市主要分布在河流沿岸及河口三角洲地区,主要原因是()①水流湍急,水能丰富②地势平坦③ 2020-12-19 …
该半岛人口和大城市主要分布在河流沿岸及河口三角洲地区,主要原因是()①水流湍急,水能丰富②地势平坦③ 2020-12-19 …