如图，已知△ABC中高AD恰好平分边BC，∠B=30°，点P是BA延长线上一点，点O是线段AD上一点且OP=OC，下面的结论：①AC=AB；②∠APO+∠DCO=30°；③△OPC是等边三角形；④AC=AO+AP．其中正确的为（

Question

如图，已知△ABC中高AD恰好平分边BC，∠B=30°，点P是BA延长线上一点，点O是线段AD上一点且OP=OC，下面的结论：
①AC=AB；②∠APO+∠DCO=30°；③△OPC是等边三角形；④AC=AO+AP．
其中正确的为（　　）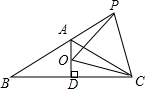

A. ①②③

B. ①②④

C. ①③④

D. ①②③④

Answer 1

∵△ABC中高AD恰好平分边BC，
∴∠ADB=∠ADC=90°，BD=CD，
在∠ABD与△ACD中，

AD=AD

∠ADB=∠ADC

BD=CD

，
∴△ABD≌△ACD（SAS），
∴AB=AC．
故①正确；
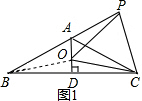
如图1，连接OB，
∵AB=AC，AD⊥BC，
∴BD=CD，∠BAD=(1)/(2)∠BAC=(1)/(2)×120°=60°，
∴OB=OC，∠ABC=90°-∠BAD=30°
∵OP=OC，
∴OB=OC=OP，
∴∠APO=∠ABO，∠DCO=∠DBO，
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°；
故②正确；
∵∠APC+∠DCP+∠PBC=180°，
∴∠APC+∠DCP=150°，
∵∠APO+∠DCO=30°，
∴∠OPC+∠OCP=120°，
∴∠POC=180°-（∠OPC+∠OCP）=60°，
∵OP=OC，
∴△OPC是等边三角形；
故③正确；
如图2，在AC上截取AE=PA，
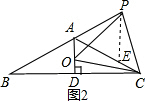∵∠PAE=180°-∠BAC=60°，
∴△APE是等边三角形，
∴∠PEA=∠APE=60°，PE=PA，
∴∠APO+∠OPE=60°，
∵∠OPE+∠CPE=∠CPO=60°，
∴∠APO=∠CPE，
∵OP=CP，
在△OPA和△CPE中，

PA=PE

∠APO=∠CPE

OP=CP

，
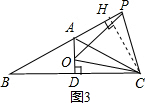
∴△OPA≌△CPE（SAS），
∴AO=CE，
∴AC=AE+CE=AO+AP；
故④正确．
故选D．