早教吧作业答案频道 -->数学-->
已知点A、B分别在x轴,y轴上,OA=OB,点C为AB的中点,AB=122(1)如图1,求点C的坐标;(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;(3)在条件(2)中,若点E的坐标为(
题目详情
已知点A、B分别在x轴,y轴上,OA=OB,点C为AB的中点,AB=12
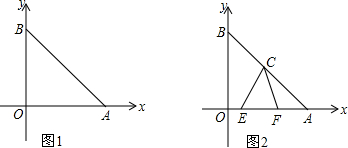
(1)如图1,求点C的坐标;
(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;
(3)在条件(2)中,若点E的坐标为(3,0),求CF的长.
| 2 |
(1)如图1,求点C的坐标;
(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;
(3)在条件(2)中,若点E的坐标为(3,0),求CF的长.

▼优质解答
答案和解析
(1)连接OC,作CM⊥OA于点M,如图1所示.
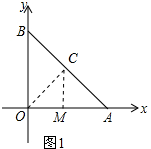
∵OA=OB,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴OA=OB=12.
∵点C为线段AB的中点,
∴OC⊥AB,
∴△OCA为等腰直角三角形,
又∵CM⊥OA,
∴CM=OM=MA=
OA=6.
故点C的坐标为(6,6).
(2)证明:连接OC,在OB上截取OM=AF,连接CM、ME,如图2所示.
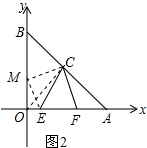
∵△AOB、△OCA、△OCB均为等腰直角三角形,
∴∠A=∠B=∠BOC=45°,OC=AC.
在△ACF和△OCM中,
,
∴△ACF≌△OCM(SAS),
∴CM=CF,∠OCM=∠ACF.
∵∠ACO=∠ACF+∠ECF+∠OCE=90°,∠ECF=45°,
∴∠ACF+∠OCE=45°=∠OCM+∠OCE=∠ECM=∠ECF.
在△ECF和△ECM中,
,
∴△ECF≌△ECM(SAS),
∴ME=EF.
在Rt△MOE中,∠MOE=90°,
∴EF2=ME2=OE2+OM2=OE2+AF2.
(3)过点C作CN⊥OA于点N,如图3所示.
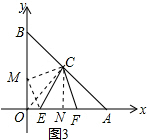
设AF=x=OM,则EF=OA-OE-AF=12-3-x=9-x=EM,
由(2)可得:(9-x)2=32+x2,
解得:x=4,
∴OF=OA-AF=12-4=8.
∵△OCA为等腰直角三角形,
∴CN=ON=
OA=6,NF=OF-ON=8-6=2.
在Rt△CNF中,∠CNF=90°,CN=6,NF=2,
∴CF=
=2
.

∵OA=OB,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴OA=OB=12.
∵点C为线段AB的中点,
∴OC⊥AB,
∴△OCA为等腰直角三角形,
又∵CM⊥OA,
∴CM=OM=MA=
| 1 |
| 2 |
故点C的坐标为(6,6).
(2)证明:连接OC,在OB上截取OM=AF,连接CM、ME,如图2所示.

∵△AOB、△OCA、△OCB均为等腰直角三角形,
∴∠A=∠B=∠BOC=45°,OC=AC.
在△ACF和△OCM中,
|
∴△ACF≌△OCM(SAS),
∴CM=CF,∠OCM=∠ACF.
∵∠ACO=∠ACF+∠ECF+∠OCE=90°,∠ECF=45°,
∴∠ACF+∠OCE=45°=∠OCM+∠OCE=∠ECM=∠ECF.
在△ECF和△ECM中,
|
∴△ECF≌△ECM(SAS),
∴ME=EF.
在Rt△MOE中,∠MOE=90°,
∴EF2=ME2=OE2+OM2=OE2+AF2.
(3)过点C作CN⊥OA于点N,如图3所示.

设AF=x=OM,则EF=OA-OE-AF=12-3-x=9-x=EM,
由(2)可得:(9-x)2=32+x2,
解得:x=4,
∴OF=OA-AF=12-4=8.
∵△OCA为等腰直角三角形,
∴CN=ON=
| 1 |
| 2 |
在Rt△CNF中,∠CNF=90°,CN=6,NF=2,
∴CF=
| CN2+NF2 |
| 10 |
看了 已知点A、B分别在x轴,y轴...的网友还看了以下:
对于任意正数a,b有f(ab)=f(a)+f(b),且f(1)的导数=1 证明f(x) 在零到正无 2020-05-13 …
f(x)具有二阶连续导数和f(x)具有连续的二阶导数有什么区别y=f(2x),其中f(x)具有二阶 2020-05-21 …
在同一对应法则f下,f(x)中的x与f[g(x)]中的g(x)两者的范围应该是一致的?在同一对应法 2020-06-12 …
数字的用处:110,112,119,114,120,121,122,12315分别在前面的电话中获 2020-06-13 …
物块静止在固定的斜面上,分别按图示的方向对物块施加大小相等的力F,A中F垂直于斜面向上.B中F垂直 2020-06-15 …
下列集合A到集合B的对应f是映射的是()A.A={-1,0,1},B={-1,0,1},f:A中的 2020-07-12 …
f(x)与f(-x)有什么关系,为什么?在函数f(x)中,当x取M时的函数值与函数f(-x)中x取 2020-07-14 …
高中数学设函数f(x),g(x)满足关系g(x)=f(x)*f(x+α)其中α是常数设函数f(x) 2020-07-27 …
下列集合A到集合B的对应f不是函数的有()①A={-1,0,1},B={-1,0,1},f:A中的 2020-07-29 …
在f(m,n)中,.m.n.f(m,n)均为非负整数且对任意的m,n有f(0,n)=n+1,f(m 2020-07-31 …