早教吧作业答案频道 -->数学-->
如图,OC是∠AOM的平分线,OD是∠BOM的平分线.(1)如图1,若∠AOB=90°,∠AOM=60°,求∠COD的度数;(2)如图2,若∠AOB=90°,∠AOM=130°,则∠COD=°;(3)如图3,若∠AOB=m°,
题目详情
如图,OC是∠AOM的平分线,OD是∠BOM的平分线.
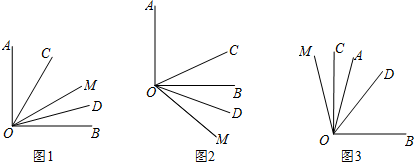
(1)如图1,若∠AOB=90°,∠AOM=60°,求∠COD的度数;
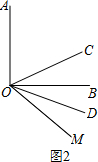
(2)如图2,若∠AOB=90°,∠AOM=130°,则∠COD=___°;
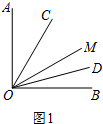
(3)如图3,若∠AOB=m°,∠AOM=n°,则∠COD=___°.

(1)如图1,若∠AOB=90°,∠AOM=60°,求∠COD的度数;
(2)如图2,若∠AOB=90°,∠AOM=130°,则∠COD=___°;
(3)如图3,若∠AOB=m°,∠AOM=n°,则∠COD=___°.
▼优质解答
答案和解析
 (1)如图1,∵∠AOB=90°,∠AOM=60°,
(1)如图1,∵∠AOB=90°,∠AOM=60°,
∴∠BOM=∠AOB-∠AOM=90°-60°=30°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=
∠AOM=
×60°=30°,
∠DOM=
∠BOM=
×30°=15°,
∴∠COD=∠COM+∠DOM=30°+15°=45°;
(2)如图2,∵∠AOB=90°,∠AOM=130°,
∴∠BOM=∠AOM-∠AOB=130°-90°=40°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=
∠AOM=
×130°=65°,
∠DOM=
∠BOM=
×40°=20°,
∴∠COD=∠COM-∠DOM=65°-20°=45°
故答案为:45.
(3)如图3,∵∠AOB=m°,∠AOM=n°,
∴∠BOM=∠AOB+∠AOM=m°+n°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=
∠AOM=
×n°=
n°,
∠DOM=
∠BOM=
(m°+n°),
∴∠COD=∠DOM-∠COM=
(m°+n°)-
n°=
m°.
故答案为:
m.

 (1)如图1,∵∠AOB=90°,∠AOM=60°,
(1)如图1,∵∠AOB=90°,∠AOM=60°,∴∠BOM=∠AOB-∠AOM=90°-60°=30°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
∠DOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COD=∠COM+∠DOM=30°+15°=45°;
(2)如图2,∵∠AOB=90°,∠AOM=130°,
∴∠BOM=∠AOM-∠AOB=130°-90°=40°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
∠DOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COD=∠COM-∠DOM=65°-20°=45°
故答案为:45.

(3)如图3,∵∠AOB=m°,∠AOM=n°,
∴∠BOM=∠AOB+∠AOM=m°+n°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠DOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COD=∠DOM-∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
看了 如图,OC是∠AOM的平分线...的网友还看了以下:
问俩道二次函数的问题1.若抛物线y=-x^+bx+c的最高点时(4,-2),则b=()c=()2. 2020-04-25 …
设直角三角形的两条直角边分别为a,b,斜边是c,周长是C,面积是S,(1)若a=根号50,b=根号 2020-05-17 …
在锐角三角形ABC中,a,bc分别为角A,B,C所对的边,a,b,c成等比数列且2sinAsinC 2020-06-03 …
八下勾股定理在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C所对的边(1)若a=5.b 2020-06-06 …
y=ax2+bx+c顶点为(2,4)(1)用含a式子表示b,c(2)若y=kx+4(k不等于0)与 2020-07-25 …
已知向量a=(3,2),b=(2,-1),c=(6,11)试用a、b表示c已知向量a=(3,2), 2020-07-25 …
1.若ax^2+bx+c可分解为(2x-1)(3x+2),则a=,b=,c=2.若a^2+m+9b 2020-07-30 …
1.已知向量a=(2,4),向量b=(-1,2),若向量c=向量a-(向量a*向量b)*向量b,求 2020-08-01 …
有4条线段是成比例线段,其中a=8cm,b=0.05cm,c=0.6cm,d=10cm,请判断他们 2020-08-02 …
已知函数f(x)=ax+b/x+c(a>0)的图像在点,(1,f(1))处的切线方程为y=x-1.( 2020-12-08 …