早教吧作业答案频道 -->数学-->
已知等腰Rt△ABC与等腰Rt△CDE,∠ACB=∠DCE=90°,把Rt△ABC绕点C旋转.(1)如图1,当点A旋转到ED的延长线时,若BC=1322,BE=5,求CD的长;(2)当Rt△ABC旋转到如图2所示的位置时,过点C作BD的垂
题目详情
已知等腰Rt△ABC与等腰Rt△CDE,∠ACB=∠DCE=90°,把Rt△ABC绕点C旋转.
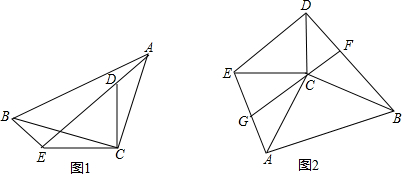
(1)如图1,当点A旋转到ED的延长线时,若BC=
,BE=5,求CD的长;
(2)当Rt△ABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.

(1)如图1,当点A旋转到ED的延长线时,若BC=
13
| ||
| 2 |
(2)当Rt△ABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.
▼优质解答
答案和解析
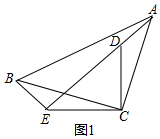 (1)如图1,∵△ADC是由△BEC绕点C旋转得到的,
(1)如图1,∵△ADC是由△BEC绕点C旋转得到的,
∴AD=BE=5,∠ADC=∠BEC,
∵在等腰Rt△ABC与等腰Rt△CDE中,BC=AC=
,∠EDC=∠DEC=45°,
∴AB=13,∠ADC=∠BEC=135°,
∴∠AEB=90°,
∴AE=
=12,
∴DE=7,
∴等腰Rt△CDE中,CD=
DE=
;
(2)如图2,过点A作AH∥CE,交CG的延长线于H,连接HE,则∠CAH+∠ACE=180°,
∵∠ACB=∠DCE=90°,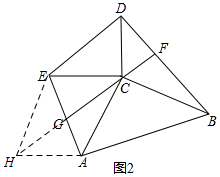
∴∠BCD+∠ACE=180°,
∴∠CAE=∠BCD,
∵CF⊥BD,∠ACB=90°,
∴∠CBF+∠BCF=∠ACG+∠BCF=90°,
∴∠CBF=∠ACG,
在△BCD和△CAH中,
,
∴△BCD≌△CAH(ASA),
∴AH=CD=CE,BD=CH,
又∵AH∥CE,
∴四边形ACEH是平行四边形,
∴CH=2CG,
∴BD=2CG.
 (1)如图1,∵△ADC是由△BEC绕点C旋转得到的,
(1)如图1,∵△ADC是由△BEC绕点C旋转得到的,∴AD=BE=5,∠ADC=∠BEC,
∵在等腰Rt△ABC与等腰Rt△CDE中,BC=AC=
13
| ||
| 2 |
∴AB=13,∠ADC=∠BEC=135°,
∴∠AEB=90°,
∴AE=
| AB2-BE2 |
∴DE=7,
∴等腰Rt△CDE中,CD=
| ||
| 2 |
7
| ||
| 2 |
(2)如图2,过点A作AH∥CE,交CG的延长线于H,连接HE,则∠CAH+∠ACE=180°,
∵∠ACB=∠DCE=90°,

∴∠BCD+∠ACE=180°,
∴∠CAE=∠BCD,
∵CF⊥BD,∠ACB=90°,
∴∠CBF+∠BCF=∠ACG+∠BCF=90°,
∴∠CBF=∠ACG,
在△BCD和△CAH中,
|
∴△BCD≌△CAH(ASA),
∴AH=CD=CE,BD=CH,
又∵AH∥CE,
∴四边形ACEH是平行四边形,
∴CH=2CG,
∴BD=2CG.
看了 已知等腰Rt△ABC与等腰R...的网友还看了以下:
正方体中证明三点共线,在正方体ABCD-A'B'C'D'中,点E、F分别是AA’、CC’的中点,连结 2020-03-30 …
1.正方形ABCD,E为BD上一点,连接AE并延长交CD于点F,交BC延长线于G,求证AE²=EF 2020-04-27 …
万用表测得一根2*1.5平方护套线的单线电阻为0.8至1欧,为何电压降却几乎为0?这是一根10米的 2020-05-16 …
先阅读以下求22.5°的解题方法:如图,构造等腰三角形ABC使∠C=90°……先阅读以下求22.5 2020-05-20 …
如图,在△ABC中,∠B=45°,点D为BA延长线上一点,作∠DAE=∠BAC,交BC延长交于点E 2020-06-22 …
已知三角形ABC,D是BC延长线上的点,F是AB延长线上的点,角ACD的平分线叫BA的延长线于E, 2020-07-11 …
如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交 2020-07-11 …
一个长方形,长和宽各增加5厘米,面积就会增加185厘米.原长方形的周长是多少厘米还有就是将一个正方 2020-07-18 …
比例线段于=与相似三角形如图在三角形abc中(1)ed平行于bc,分别交ab、ac于e、d,bd、 2020-07-24 …
已知圆O是三角形ABC的外接圆,AB是圆O的直径,D是AB延长线上的一点,AE垂直于DC交DC的延 2020-08-01 …