早教吧作业答案频道 -->数学-->
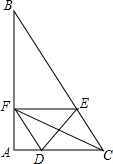
如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A开始以1cm/s的速度向点C运动,点E从点C开始以2cm/s的速度向点B运动,两点同时运动,同时停止,运动的时间为ts,过点E作EF∥AC交AB于点F.
题目详情
如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A开始以1cm/s的速度向点C运动,点E从点C开始以2cm/s的速度向点B运动,两点同时运动,同时停止,运动的时间为ts,过点E作EF∥AC交AB于点F.
(1)当t为何值时,△DEC为等边三角形?
(2)当t为何值时,△DEC为直角三角形?
(3)求证:DC=EF.
(4)连接CF,当CF平分∠ACB时,直接写出AF与BF之间的数量关系.

(1)当t为何值时,△DEC为等边三角形?
(2)当t为何值时,△DEC为直角三角形?
(3)求证:DC=EF.
(4)连接CF,当CF平分∠ACB时,直接写出AF与BF之间的数量关系.
▼优质解答
答案和解析
由题意得AD=tcm,CE=2tcm,
(1)若△DEC为等边三角形,则EC=DC,
∴2t=6-t,解得t=2,
∴当t为2时,△DEC为等边三角形;
(2)若△DEC为直角三角形,当∠CED=90°,
∴CE=
DC,
∴2t=
(6-t),
解得:t=1.2,
当∠CDE=90°时,∴
CE=DC,
∴
×2t=6-t,
∴t=3,
∴t为1.2或3时,△DEC为直角三角形;
(3)∵∠A=90°,∠B=30°,AC=6cm,∴BC=12cm,∴DC=(6-t)cm,BE=(12-2T)cm,∵EF∥AC,∴∠A=∠BFE=90°,∵∠B=30°,∴EF=
BE=
(12-2t)=(6-t)cm,∴EF=CD,(4)∵∠A=90°,∠B=30°,∴∠ACB=60°,∵CF平分∠ACB,
∴∠ACF=∠BCF=30°,
∴∠B=∠BCF,AF=
CF,
∴BF=CF,
∴BF=2AF.
(1)若△DEC为等边三角形,则EC=DC,
∴2t=6-t,解得t=2,
∴当t为2时,△DEC为等边三角形;
(2)若△DEC为直角三角形,当∠CED=90°,
∴CE=
| 1 |
| 2 |
∴2t=
| 1 |
| 2 |
解得:t=1.2,
当∠CDE=90°时,∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴t=3,
∴t为1.2或3时,△DEC为直角三角形;
(3)∵∠A=90°,∠B=30°,AC=6cm,∴BC=12cm,∴DC=(6-t)cm,BE=(12-2T)cm,∵EF∥AC,∴∠A=∠BFE=90°,∵∠B=30°,∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ACF=∠BCF=30°,
∴∠B=∠BCF,AF=
| 1 |
| 2 |
∴BF=CF,
∴BF=2AF.
看了 如图,在△ABC中,∠A=9...的网友还看了以下:
向量(x,y,z)和点(a,b,c)的距离怎么求,公式是什么?过原点和(x,y,z)两点的向量应该 2020-04-07 …
给出如下命题:①向量AB的长度与向量BA的长度相等;②向量a与b平行,则a与b的方向相同或相反;③ 2020-04-08 …
给出下列命题①向量AB的长度与向量BA的长度相等;②向量a与向量b平行,则a与b的方向相同或相反; 2020-04-08 …
在平行六面体ABCD-A'B'C'D'中,向量、、、是A有相同起点的向量B等长的向量C共面向量D不 2020-05-13 …
如图所示,A、B是一条电场线上的两点,一带正电的粒子在电场力作用下由A点静止释放,运动到B点,则( 2020-05-15 …
如图所示的杠杆处于平衡,把A端所挂重物浸没在水中,杠杆将失去平衡,为使杠杆重新平衡应()A.将支点 2020-05-16 …
初中数学关于一元二次方程及动点问题,在线等待今晚就要!在直角三角形中,AC为斜边,角B为90°,P 2020-05-23 …
起点在坐标原点的向量叫做定位向量或位置向量,其坐标等于它的什么坐标;向量的坐标等于它的什么坐标减. 2020-06-14 …
在静电场中,将一电子从A点移到B点,电场力做了正功,则A.电场强度的方向一定是由A点指向B点B.电 2020-06-17 …
如图所示,压路机大轮的半径R是小轮半径r的2倍.压路机匀速行驶时,大轮边缘上A点的向心加速度是12 2020-06-17 …