早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠BAC=106°,MP,NQ分别垂直平分AB,AC.(1)当AB=AC时,∠1的度数为.(2)若AB≠AC,请问(1)中的结论还成立吗?请通过计算说明.
题目详情
如图,在△ABC中,∠BAC=106°,MP,NQ分别垂直平分AB,AC.
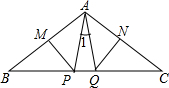
(1)当AB=AC时,∠1的度数为___.
(2)若AB≠AC,请问(1)中的结论还成立吗?请通过计算说明.

(1)当AB=AC时,∠1的度数为___.
(2)若AB≠AC,请问(1)中的结论还成立吗?请通过计算说明.
▼优质解答
答案和解析
(1)∵∠BAC=106°,
∴∠ABP+∠ACQ=180°-105°=74°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=74°,
∴∠1=106°-74°=32°;
故答案为:32°;
(2)成立,
理由:∵∠BAC=106°,
∴∠ABP+∠ACQ=180°-105°=74°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=74°,
∴∠1=106°-74°=32°.
∴∠ABP+∠ACQ=180°-105°=74°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=74°,
∴∠1=106°-74°=32°;
故答案为:32°;
(2)成立,
理由:∵∠BAC=106°,
∴∠ABP+∠ACQ=180°-105°=74°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=74°,
∴∠1=106°-74°=32°.
看了如图,在△ABC中,∠BAC=...的网友还看了以下:
试述厨房劳动组织管理的内容(简答题试举例说明)a.首先论述劳动组织管理的内容?b.厨房岗位组织结构 2020-07-14 …
所有具体科学的发展最终都可以归结于哲学的进步。这表明()A.哲学是世界观和方法论的统一B.哲学是对 2020-08-03 …
辩论赛无人监考利大于弊还是弊大于利求正反两方的资料或者提供一段此辩题的视频需要一辩的开篇呈辞和四辩的 2020-11-06 …
求对荣格情结理论的深入理解《分析心理学的理论与实践》P77,情结与意志的关系情结是联想的凝聚:一种多 2020-11-21 …
毛泽东思想是()A.马克思列宁主义在中国的运用和发展B.被实践证明了的关于中国革命和建设的正确理论原 2020-12-03 …
康德的伦理学是什么?A.动机论B.手段论C.结果论D.工具论 2020-12-13 …
数据结构论述题,假设在树中,结点x是结点y的双亲时,用(x,y)来表示树边.已知一棵树边的集合为:{ 2020-12-23 …
关于贵州省的生态文明建设主题的论文2000字运用理论知识结合实际全面展开分析的论述,要归纳和总结出论 2020-12-23 …
题目《格式塔组织原则在环境设计中的应用》或《基于生态知觉理论的xxxx设计》求一篇结可论文要求300 2020-12-23 …
结果论,非结果论,美德论的道德定义 2020-12-23 …