早教吧作业答案频道 -->数学-->
已知:在△ABC中,∠BAC=60°.(1)如图1,若AB=AC,点P在△ABC内,且PB=5,PA=3,PC=4,直接写出∠APC的度数.(2)如图2,若AB=AC,点P在△ABC外,且PA=3,PB=5,PC=4,求∠APC的度数;(3)如图3,
题目详情
已知:在△ABC中,∠BAC=60°.
(1)如图1,若AB=AC,点P在△ABC内,且PB=5,PA=3,PC=4,直接写出∠APC的度数.
(2)如图2,若AB=AC,点P在△ABC外,且PA=3,PB=5,PC=4,求∠APC的度数;
(3)如图3,若AB=2AC,点P在△ABC内,且PA=
,PB=5,∠APC=120°,直接写出PC的长.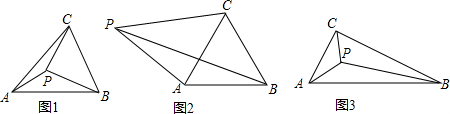
(1)如图1,若AB=AC,点P在△ABC内,且PB=5,PA=3,PC=4,直接写出∠APC的度数.
(2)如图2,若AB=AC,点P在△ABC外,且PA=3,PB=5,PC=4,求∠APC的度数;
(3)如图3,若AB=2AC,点P在△ABC内,且PA=
| 3 |

▼优质解答
答案和解析
(1)把△APC绕着点A顺时针旋转,使点C旋转到点B,得到△ADB,连结DP.
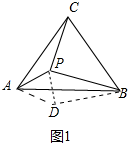
由旋转可知AD=AP,BD=PC,∠DAB=∠PAC,
∴∠DAP=∠BAC=60°,
∴△ADP为等边三角形,
∴DP=PA=3,∠ADP=60°,
∵PB=5,BD=PC=4,PD=3,
∴PD2+BD2=PB2
∴∠BDP=90°,
∴∠APC=∠ADB=∠ADP+∠PDB=60°+90°=150°.
(2)如图2,
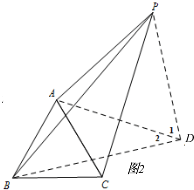
把△APC绕点A顺时针旋转,使点C与点B重合,得到△ADB,连接PD,
∴△APC≌△ADB,
∴AD=AP=3,DB=PC=4,∠PAC=∠DAB,∠APC=∠2,
∴∠DAP=∠BAC,
∵∠BAC=60°,
∴∠DAP=60°,
∴△DAP是等边三角形,
∴PD=3,∠1=60°,
∴PD2+DB2=32+42=52=PB2,
∴∠PDB=90°,
∴∠2=30°,
∴∠APC=30°;
(3)如图3
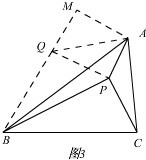
作△ABQ,使得:∠QAB=∠PAC,∠ABQ=∠ACP,则△ABQ∽△ACP,
∴∠AQB=∠APC=120°,
∵AB=2AC,
∴△ABQ与△ACP相似比为2,
∴AQ=2AP=2
,BQ=2CP,∠QAP=∠QAB+∠BAP=∠PAC+∠BAP=∠BAC=60°,
∵
=2,
∴∠APQ=90°,PQ=3,
∴∠AQP=30°
∴∠BQP=∠AQB-∠AQP=120°-30°=90°,
根据勾股定理得,BQ=
=4,
∴PC=
BQ=2.

由旋转可知AD=AP,BD=PC,∠DAB=∠PAC,
∴∠DAP=∠BAC=60°,
∴△ADP为等边三角形,
∴DP=PA=3,∠ADP=60°,
∵PB=5,BD=PC=4,PD=3,
∴PD2+BD2=PB2
∴∠BDP=90°,
∴∠APC=∠ADB=∠ADP+∠PDB=60°+90°=150°.
(2)如图2,

把△APC绕点A顺时针旋转,使点C与点B重合,得到△ADB,连接PD,
∴△APC≌△ADB,
∴AD=AP=3,DB=PC=4,∠PAC=∠DAB,∠APC=∠2,
∴∠DAP=∠BAC,
∵∠BAC=60°,
∴∠DAP=60°,
∴△DAP是等边三角形,
∴PD=3,∠1=60°,
∴PD2+DB2=32+42=52=PB2,
∴∠PDB=90°,
∴∠2=30°,
∴∠APC=30°;
(3)如图3

作△ABQ,使得:∠QAB=∠PAC,∠ABQ=∠ACP,则△ABQ∽△ACP,
∴∠AQB=∠APC=120°,
∵AB=2AC,
∴△ABQ与△ACP相似比为2,
∴AQ=2AP=2
| 3 |
∵
| AQ |
| AP |
∴∠APQ=90°,PQ=3,
∴∠AQP=30°
∴∠BQP=∠AQB-∠AQP=120°-30°=90°,
根据勾股定理得,BQ=
| PB2-PQ2 |
∴PC=
| 1 |
| 2 |
看了 已知:在△ABC中,∠BAC...的网友还看了以下:
如图,一次函数y=-2/3x+2的图像分别与x轴和y轴交与点A和B,以线段AB为边在第一象限内,作 2020-04-05 …
已知三角形ABC的三个顶点,A,B,C及平面一点P,满足向量PA+向量PB+向量PC=向量AB,则 2020-04-27 …
已知:inta[]={1,2,3,4,5,6,7,8,9,10,11,12},*p=a则值为3的表 2020-05-13 …
已知三角形ABC的三个顶点A,B,C及所在平面内一点P满足PA向量+PB向量+PC向量=AB向量, 2020-05-13 …
在平面直角坐标系中,知点A(0,4),B(4,0),P为函数y=8/x(x>0)图象上一点,过点P 2020-06-14 …
延长⊙O的直径AB到P,使PB=OB,过P作PC切⊙O于C,过B作BD切⊙O于B,交PC于D.(1 2020-07-24 …
圆心A和圆心B是外离两圆,圆心A的半径为4,圆心B的半径为2,AB=8,P在AB上,PC切圆心A于 2020-07-26 …
1.已知A={(x,y)|y/1-x平方=1},B={(x,y)|y=1-x平方},C={(x,y 2020-08-01 …
设A,B,C为非空集合,M=A∩C,N=B∩C,P=M∪N,则必有()A.C∩P=CB.C∩P=P 2020-08-01 …
(2012•台州一模)如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=43,B 2020-08-02 …