早教吧作业答案频道 -->数学-->
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=3,BC=4,点E在AB边上,BE=3,∠CED=90°.(1)求CE的长度;(2)求证:△ADE≌△BEC;(3)设点P是线段AB上的一个动点,求DP+CP的最小值是多少
题目详情
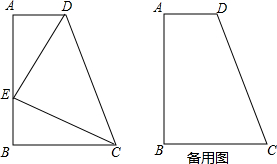 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=3,BC=4,点E在AB边上,BE=3,∠CED=90°.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=3,BC=4,点E在AB边上,BE=3,∠CED=90°.(1)求CE的长度;
(2)求证:△ADE≌△BEC;
(3)设点P是线段AB上的一个动点,求DP+CP的最小值是多少?
▼优质解答
答案和解析
考点:
全等三角形的判定与性质 勾股定理 轴对称-最短路线问题
专题:
分析:
(1))由∠B=90°,BC=4,BE=3,根据勾股定理求出CE;(2)先证出∠DEA=∠ECB,即可证明△ADE≌△BEC;(3)作点D关于AB的对称点F,连接CF交AB于点P,再用勾股定理求出CF的长即为DP+CP的最小值.
(1)∵∠B=90°,BC=4,BE=3,根据勾股定理可得:CE=BC2+BE2=42+32=5;(2)∵∠CED=90°,∴∠CEB+∠DEA=90°,∵∠B=90°,∴∠CEB+∠ECB=90°,∴∠DEA=∠ECB,∵AD∥BC,∠B=90°,∴∠A=∠B=90°,在△ADE和△BEC中,DEA=∠ECB ∠A=∠B AD=BE ∴△ADE≌△BEC(AAS);(3)延长DA至F,使得AD=AF,并连接CF,此时CF与AB的交点为点P,连接PD;∵AB⊥AD,且AD=AF,∴△DFP是等腰三角形,∴DP=FP,∴DP+CP的最小值为CF,过点F作FH垂直CB的长线,垂足为H,如图所示:根据题意得:CH=7,FH=7,根据勾股定理可得,CF=72+72=72,即DP+CP的最小值为72.
点评:
本题考查了勾股定理、轴对称以及最短路线问题;熟练掌握勾股定理和最短路线的作图是解决问题的关键.
考点:
全等三角形的判定与性质 勾股定理 轴对称-最短路线问题
专题:
分析:
(1))由∠B=90°,BC=4,BE=3,根据勾股定理求出CE;(2)先证出∠DEA=∠ECB,即可证明△ADE≌△BEC;(3)作点D关于AB的对称点F,连接CF交AB于点P,再用勾股定理求出CF的长即为DP+CP的最小值.
(1)∵∠B=90°,BC=4,BE=3,根据勾股定理可得:CE=BC2+BE2=42+32=5;(2)∵∠CED=90°,∴∠CEB+∠DEA=90°,∵∠B=90°,∴∠CEB+∠ECB=90°,∴∠DEA=∠ECB,∵AD∥BC,∠B=90°,∴∠A=∠B=90°,在△ADE和△BEC中,DEA=∠ECB ∠A=∠B AD=BE ∴△ADE≌△BEC(AAS);(3)延长DA至F,使得AD=AF,并连接CF,此时CF与AB的交点为点P,连接PD;∵AB⊥AD,且AD=AF,∴△DFP是等腰三角形,∴DP=FP,∴DP+CP的最小值为CF,过点F作FH垂直CB的长线,垂足为H,如图所示:根据题意得:CH=7,FH=7,根据勾股定理可得,CF=72+72=72,即DP+CP的最小值为72.
点评:
本题考查了勾股定理、轴对称以及最短路线问题;熟练掌握勾股定理和最短路线的作图是解决问题的关键.
看了 如图,在四边形ABCD中,A...的网友还看了以下:
物质的量浓度相同的naclmgcl2alcl3三种溶液,当溶液的体积比为3:2:1时,三种溶液中c 2020-04-26 …
如图1,A为轴负半轴上一点,点B为x轴正半轴上一点,C(0,-2),D(-3,-2).(1)求三角 2020-04-26 …
这个公式怎么理解|如题:=IF(ISERROR(IF(SUMIF(INDIRECT("'"&D$3 2020-05-23 …
已知幂函数Y=X的(M的平方-M-6)次幂.(M属于整数)的图像与X轴无公共点,则M的取值范围是( 2020-06-03 …
圆X^2+Y^2-2y=3上的点到直线x-y-5=0的距离的最大值为()选项A.3√2+1 B.3 2020-06-27 …
要求质量拜托了!钱随便开.前四题选择,后几道填空1.函数f(x)=sinx-|sinx|的值域为? 2020-07-23 …
过点A(0,7/3)与点B(7,0)的直线L1与过点C((2,1),D(3,K+1)D的直线L2和 2020-07-31 …
高三数列的极限题首项为1的无穷等比数列{an}的各项之和为S,前n项和为Sn,且n趋于无穷时,(S 2020-08-02 …
已知A(1,0,4)、B(0,-1,3)、C(1,2,-2)、D(-3,2,1)处分别有力F1(5i 2020-11-01 …
已知全集U=Z,Z为整数集,如图程序框图所示,集合A={x|框图中输出的x值},B={y|框图中输出 2021-01-15 …