如图1为放置在水平桌面上的台灯的平面示意图，灯臂AO长为50cm，与水平桌面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平桌面所形成的夹角∠OCA，∠OBA分别为90°和30°．（不

Question

如图1为放置在水平桌面上的台灯的平面示意图，灯臂AO长为50cm，与水平桌面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平桌面所形成的夹角∠OCA，∠OBA分别为90°和30°．（不考虑其他因素，结果精确到0.1cm． sin75°≈0.97，cos75°≈0.26，√(3)≈1.73

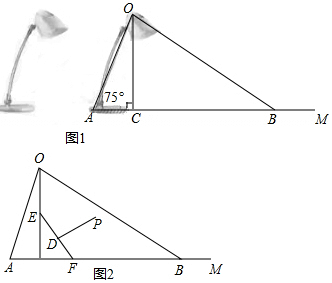
（1）求该台灯照亮水平桌面的宽度BC．
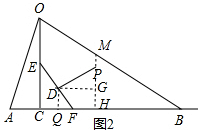
（2）人在此台灯下看书，将其侧面抽象成如图2所示的几何图形，若书与水平桌面的夹角∠EFC为60°，书的长度EF为24cm，点P为眼睛所在位置，当点P在EF 的垂直平分线上，且到EF距离约为34cm（人的正确看书姿势是眼睛离书距离约1尺≈34cm）时，称点P为“最佳视点”．请通过计算说明最佳视点P在不在灯光照射范围内？

Answer 1

（1）在直角三角形ACO中，sin75°=(OC)/(OA)，
解得OC=50×0.97≈48.5，
在直角三角形BCO中，tan30°=(OC)/(BC)，
解得BC=1.73×48.5≈83.9．
答：该台灯照亮水平面的宽度BC大约是83.9cm，

（2）如图，过点P作PH⊥AB于H，交OB于M，过点D作DG⊥PH于G，DQ⊥AB于Q，则四边形DGHQ为矩形，∠GDF=∠EFC=∠DPG=60°
由题意DE=DF=12，DP=34，
∴PG=17，QH=DG=17√(3)，QF=6，GH=DQ=6√(3)，
∴PH=PH+GH=17+6√(3)≈27.38，
又∵CH=6+17√(3)≈35.41 
∴HB=CB-CH=83.9-35.41≈48.49，
∵∠OBC=30°，tan∠OBC=1：√(3)，
∴MH=HB÷√(3)=48.49÷√(3)≈28.03，
∵27.38<28.03，
∴最佳视点P在灯光照射范围内．