如图，边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上，顶点C、D在圆内，将正方形ABCD沿圆的内壁作无滑动的滚动．当滚动一周回到原位置时，点C运动的路径长为（）A.22πB.（2+1

Question

如图，边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上，顶点C、D在圆内，将正方形ABCD沿圆的内壁作无滑动的滚动．当滚动一周回到原位置时，点C运动的路径长为（　　）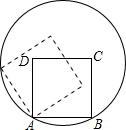

A. 2

√(2)π

B. （

√(2)+1）π

C. （

√(2)+2）π

D. （

(2)/(3)√(2)+1）π

Answer 1

如图，分别连接OA、OB、OD′、OC、OC′；
∵OA=OB=AB，
∴△OAB是等边三角形，
∴∠OAB=60°；
同理可证：∠OAD′=60°，
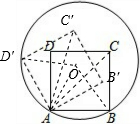
∴∠D′AB=120°；
∵∠D′AB′=90°，
∴∠BAB′=120°-90°=30°，
由旋转变换的性质可知∠C′AC=∠B′AB=30°；
∵四边形ABCD为正方形，且边长为2，
∴∠ABC=90°，AC=√(22+22)=2√(2)，
∴当点D第一次落在圆上时，点C运动的路线长为：(30π×2√(2))/(180)=(√(2)π)/(3)．
以D或B为圆心滚动时，每次C点运动(π)/(3)，
以A做圆心滚动两次，以B和D做圆心滚动三次，所以总路径=(√(2)π)/(3)×2+(π)/(3)×3=（(2)/(3)√(2)+1）π．
故选：D．