早教吧作业答案频道 -->数学-->
如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.(1)求∠CDB的度数;(2)求证:△DCA∽△DAB;(3)若CD的长为1,求AB的长.
题目详情
如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.
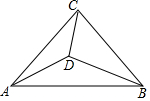
(1)求∠CDB的度数;
(2)求证:△DCA∽△DAB;
(3)若CD的长为1,求AB的长.

(1)求∠CDB的度数;
(2)求证:△DCA∽△DAB;
(3)若CD的长为1,求AB的长.
▼优质解答
答案和解析
(1) ∵△ABC为等腰直角三角形,
∴∠CAB=45°.
又∵∠ACD=∠DAB,
∴∠ACD+∠CAD=∠DAB+∠CAD=∠CAB=45°,
∴∠CDA=135°
同理可得∠ADB=135°
∴∠CDB=360°-∠CDA-∠ADB=360°-135°-135°=90°.
(2)证明:∵∠CDA=∠ADB,∠ACD=∠DAB,
∴△DCA∽△DAB
(3) ∵△DCA∽△DAB,
∴
=
=
=
,
又∵CD=1,
∴AD=
,DB=2.
又∵∠CDB=90°,
∴BC=
=
=
,
在Rt△ABC中,∵AC=BC=
,
∴AB=
=
.
∴∠CAB=45°.
又∵∠ACD=∠DAB,
∴∠ACD+∠CAD=∠DAB+∠CAD=∠CAB=45°,
∴∠CDA=135°

同理可得∠ADB=135°
∴∠CDB=360°-∠CDA-∠ADB=360°-135°-135°=90°.
(2)证明:∵∠CDA=∠ADB,∠ACD=∠DAB,
∴△DCA∽△DAB
(3) ∵△DCA∽△DAB,
∴
| DC |
| DA |
| DA |
| DB |
| AC |
| BA |
| 1 | ||
|
又∵CD=1,
∴AD=
| 2 |
又∵∠CDB=90°,
∴BC=
| CD2+BD2 |
| 12+22 |
| 5 |
在Rt△ABC中,∵AC=BC=
| 5 |
∴AB=
| AC2+BC2 |
| 10 |
看了 如图,在等腰直角△ABC中,...的网友还看了以下:
如图,在正方形ABCD中,已知A、B两点的坐标分别是A(1,0)B(根号二+1,0).①求C、D两 2020-05-13 …
在海拔为500m的海岛A处,测得海面上两船C、D的俯角分别为45°和30°,又测得∠CAD=135 2020-05-16 …
已知:∠A=(90+x)°,∠B=(90-x)°,∠CED=90°,射线EF∥AC,2∠C-∠D= 2020-06-12 …
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d的图象如图所示(1)求c,d的值;(2) 2020-07-16 …
已知b/a=(4d-7)/c,(b+1)/a=7(d-1)/c,求c/a=?,d/b=?a,b,c 2020-07-19 …
如图,在直角坐标系中,Rt△AOB的顶点坐标分别为A(0,2),O(0,0),B(4,0),△AO 2020-07-19 …
如图,在平面直角坐标系中Rt△AOB的顶角坐标分别为A(-2,0),O(0,0),B(0,4),把 2020-07-24 …
如图所示,在平面直角坐标系中,Rt△AOB的顶点坐标分别为A(-2,0),O(0,0),B(0,4 2020-08-02 …
(2013•汕头)已知二次函数y=x2-2mx+m2-1.(1)当二次函数的图象经过坐标原点O(0, 2020-11-12 …
如图,为了测不可到达的河北岸C,D之间的距离,在河南岸选定A,B两点,测得AB=100米,∠CAD= 2021-01-02 …