早教吧作业答案频道 -->数学-->
如图,在△ABC中,AD为内角平分线,∠ADC=60°,点E在AD上,满足DE=DB,射线CE交AB于点F,求证:AF•AB+CD•CB=AC2.
题目详情
如图,在△ABC中,AD为内角平分线,∠ADC=60°,点E在AD上,满足DE=DB,射线CE交AB于点F,求证:AF•AB+CD•CB=AC2.

▼优质解答
答案和解析
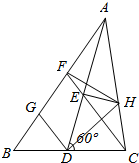 证明:如图,作∠ADG=∠ADC=60°,交AB于G,则∠BDG=60°,
证明:如图,作∠ADG=∠ADC=60°,交AB于G,则∠BDG=60°,
在△ADG和△ADC中,
∠DAG=∠DAC,AD=AD,∠ADG=∠ADC,
∴△ADG≌△ADC,∴DG=DC,
∵DE=DB,∠BDG=∠EDC=60°,
∴△BDG≌△DEC,∴∠BGD=∠DCE,∴∠BFC=∠ADC=60°,
∴∠B=∠DEC=∠FEA,
∴B、D、E、F四点共圆,∴AF•AB=AE•AD,
在AC上取点H,使得CD•CB=CH•CA,
则B、D、H、F四点共圆,
∴∠B=∠CHD,又∠B=∠DEC,∴∠DEC=∠CHD,
∴D、C、H、E四点共圆,
∴AE•AD=AH•AC,
∵CD•CB=CH•CA=CA•(CA-AH)=CA2-CA•AH,
∴AF•AB+CD•CB=AC2.
 证明:如图,作∠ADG=∠ADC=60°,交AB于G,则∠BDG=60°,
证明:如图,作∠ADG=∠ADC=60°,交AB于G,则∠BDG=60°,在△ADG和△ADC中,
∠DAG=∠DAC,AD=AD,∠ADG=∠ADC,
∴△ADG≌△ADC,∴DG=DC,
∵DE=DB,∠BDG=∠EDC=60°,
∴△BDG≌△DEC,∴∠BGD=∠DCE,∴∠BFC=∠ADC=60°,
∴∠B=∠DEC=∠FEA,
∴B、D、E、F四点共圆,∴AF•AB=AE•AD,
在AC上取点H,使得CD•CB=CH•CA,
则B、D、H、F四点共圆,
∴∠B=∠CHD,又∠B=∠DEC,∴∠DEC=∠CHD,
∴D、C、H、E四点共圆,
∴AE•AD=AH•AC,
∵CD•CB=CH•CA=CA•(CA-AH)=CA2-CA•AH,
∴AF•AB+CD•CB=AC2.
看了 如图,在△ABC中,AD为内...的网友还看了以下:
设A,B是数域P上两个n阶矩阵,A^n=B^n=0,但A^(n-1)不等于0,A^(n-1)不等于 2020-05-14 …
已知a>0,b>0,求证b²÷a+a²÷b>=a+b 2020-05-15 …
用柯西不等式证明:已知a、b>0求证 b/a²+a/b²≥1/a+1/b 2020-05-15 …
1三角形ABC三边a b c 求证cX²-(a+b)x+c/4=0有二个不相等的实数根2三角形AB 2020-05-16 …
已知K(xa-x2)^2≤(x1-x2)(f(x1)-f(x2))和∣f(x1)-f(x2)∣≤∣ 2020-05-17 …
设f(x)=ax²+bx+c(a,b,c∈R,a≠0)f(x)在区间[-2,2]上的最大值最小值分 2020-06-02 …
设A,B为正交矩阵,且|A|+|B|=0,证明|A+B|=0 2020-06-16 …
关于A=0的证明设A是n阶实对称矩阵,且A²=0证明A=0.其中一种证明方法是这样的:由A(T)A= 2020-11-03 …
问一道矩阵的问题A是n阶实对称矩阵,且A^2=0,证明A=0书上的证法是:因为A是实对称矩阵,A必可 2020-11-03 …
设f‘’(x)<0,a,b>0,证f(a+b)+f(0)<f(a)+f(b) 2020-11-03 …