早教吧作业答案频道 -->数学-->
如图,长方形ABCD,AB=18,AD=8,E为CD边上一点,CE=12,(1)则AE=;(2)点P从点B出发,以每秒2个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t为何值时,△PAE为
题目详情
如图,长方形ABCD,AB=18,AD=8,E为CD边上一点,CE=12,
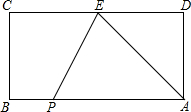
(1)则AE=___;
(2)点P从点B出发,以每秒2个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t为何值时,△PAE为等腰三角形?

(1)则AE=___;
(2)点P从点B出发,以每秒2个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t为何值时,△PAE为等腰三角形?
▼优质解答
答案和解析
(1)∵四边形ABCD是长方形,
∴∠D=90°,AB=CD=18,
∵CE=12,
∴DE=6,
在Rt△ADE中,∠D=90°,AD=8,DE=6,由勾股定理得:AE=
=10,
故答案为:10;
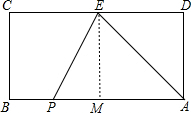
(2)过E作EM⊥AB于M,
则AM=DE=6,
若△PAE是等腰三角形,则有三种可能:
当EP=EA时,AP=2DE=12,
所以t=
=
=3;
当AP=AE=10时,BP=18-10=8,
所以t=8÷2=4;
当PE=PA时,则(12-2t)2+82=(18-2t)2,
解得:t=
.
综合上述:符合要求的t值为3或4或
.
∴∠D=90°,AB=CD=18,
∵CE=12,
∴DE=6,
在Rt△ADE中,∠D=90°,AD=8,DE=6,由勾股定理得:AE=
| 82+62 |
故答案为:10;

(2)过E作EM⊥AB于M,
则AM=DE=6,
若△PAE是等腰三角形,则有三种可能:
当EP=EA时,AP=2DE=12,
所以t=
| BP |
| 2 |
| 18-12 |
| 2 |
当AP=AE=10时,BP=18-10=8,
所以t=8÷2=4;
当PE=PA时,则(12-2t)2+82=(18-2t)2,
解得:t=
| 29 |
| 6 |
综合上述:符合要求的t值为3或4或
| 29 |
| 6 |
看了 如图,长方形ABCD,AB=...的网友还看了以下:
如图表示两种群落在演替过程中物种多样性的变化曲线,结合图示判断下列说法错误的是()A.图中表示初生 2020-05-02 …
磁铁的磁力如图:我的磁铁只能在A和E点吸上曲别针 如何能让B、D甚至C点都能吸上少量的曲别针 2020-05-14 …
如图,平行四边形AOBC中,对角线交于点E,双曲线y=kx(k>0)经过A,E两点,若平行四边形A 2020-06-12 …
(2013•上海)如图所示的E,F,P,Q四点中,磁场最强的是()A.E点B.F点C.P点D.Q点 2020-06-12 …
读图,完成28~30题.若O为北极点,H、P为晨昏线与某纬线的两个交点,则E点的时间可能为()A. 2020-07-12 …
如图,AB是⊙O的直径,点E是AB上的一点,CD是过E点的弦,过点B的切线交AC的延长线于点F,BF 2020-11-03 …
(2014•龙岩)如图是条形磁体的磁感线分布,图中的E、F、P、Q四点,磁场最强的是()A.E点B. 2020-11-12 …
读图,完成10-12题.若O为北极点,H、P为晨昏线与某纬线的两交点,则E点的时间可能为()A.5月 2020-11-27 …
i图甲,小明骑自行车经过A到E点时,每隔l.2s记录下对应点到A点的距离,在图乙坐标图中画出小明运动 2021-01-15 …
如图所示,在棱长为6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点, 2021-01-22 …