早教吧作业答案频道 -->数学-->
如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°,(1)请问△ACD是直角三角形吗?为什么?(2)四边形ABCD
题目详情
如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°,
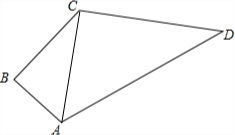
(1)请问△ACD是直角三角形吗?为什么?
(2)四边形ABCD的面积是多少?


(1)请问△ACD是直角三角形吗?为什么?
(2)四边形ABCD的面积是多少?

▼优质解答
答案和解析
(1)△ACD是直角三角形,
理由是:由题意可知:在Rt△ABC中,由勾股定理得:
AC=
=
=5,
∵AC2+CD2=52+122=169,AD2=132=169,
∴AC2+CD2=AD2,
∴∠ACD=90°,
即△ACD是直角三角形;
(2)S四边形ABCD=S△ABC+S△ACD
=
×AB×BC+
×AC×DC
=
×3×4+
×5×12
=36,
即四边形ABCD的面积是36.
AB2+BC2 AB2+BC2 AB2+BC2 AB2+BC22+BC22=
=5,
∵AC2+CD2=52+122=169,AD2=132=169,
∴AC2+CD2=AD2,
∴∠ACD=90°,
即△ACD是直角三角形;
(2)S四边形ABCD=S△ABC+S△ACD
=
×AB×BC+
×AC×DC
=
×3×4+
×5×12
=36,
即四边形ABCD的面积是36.
32+42 32+42 32+42 32+422+422=5,
∵AC22+CD22=522+1222=169,AD22=1322=169,
∴AC22+CD22=AD22,
∴∠ACD=90°,
即△ACD是直角三角形;
(2)S四边形ABCD四边形ABCD=S△ABC△ABC+S△ACD△ACD
=
×AB×BC+
×AC×DC
=
×3×4+
×5×12
=36,
即四边形ABCD的面积是36.
1 2 1 1 12 2 2×AB×BC+
×AC×DC
=
×3×4+
×5×12
=36,
即四边形ABCD的面积是36.
1 2 1 1 12 2 2×AC×DC
=
×3×4+
×5×12
=36,
即四边形ABCD的面积是36.
1 2 1 1 12 2 2×3×4+
×5×12
=36,
即四边形ABCD的面积是36.
1 2 1 1 12 2 2×5×12
=36,
即四边形ABCD的面积是36.
理由是:由题意可知:在Rt△ABC中,由勾股定理得:
AC=
| AB2+BC2 |
| 32+42 |
∵AC2+CD2=52+122=169,AD2=132=169,
∴AC2+CD2=AD2,
∴∠ACD=90°,
即△ACD是直角三角形;
(2)S四边形ABCD=S△ABC+S△ACD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=36,
即四边形ABCD的面积是36.
| AB2+BC2 |
| 32+42 |
∵AC2+CD2=52+122=169,AD2=132=169,
∴AC2+CD2=AD2,
∴∠ACD=90°,
即△ACD是直角三角形;
(2)S四边形ABCD=S△ABC+S△ACD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=36,
即四边形ABCD的面积是36.
| 32+42 |
∵AC22+CD22=522+1222=169,AD22=1322=169,
∴AC22+CD22=AD22,
∴∠ACD=90°,
即△ACD是直角三角形;
(2)S四边形ABCD四边形ABCD=S△ABC△ABC+S△ACD△ACD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=36,
即四边形ABCD的面积是36.
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=36,
即四边形ABCD的面积是36.
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=36,
即四边形ABCD的面积是36.
| 1 |
| 2 |
| 1 |
| 2 |
=36,
即四边形ABCD的面积是36.
| 1 |
| 2 |
=36,
即四边形ABCD的面积是36.
看了 如图,某住宅小区在施工过程中...的网友还看了以下:
如图,在四边形ABCD中,点E、F是对角线BD上的两点,且BE=DF.(1)若四边形AECF是平行 2020-05-01 …
①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③在四边 2020-05-14 …
如图所示,在平行四边形abcd中,点ef是对角线bd上的两点,且be=df.①若四边形aecf是平 2020-05-15 …
如图,在四边形ABCD中,AC=6,BD=8且AC⊥BD顺次连接四边形ABCD各边中点,得到四边形 2020-05-16 …
已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,BO=DO. 求证:四边形 2020-05-16 …
已知平行四边形ABCD对角线的交点为O,点E,F分别在边AB,CD上,分别沿DE,BF折叠四边形A 2020-05-16 …
初二数学,关于平行四边形在四边形ABCD中,E、F分别为AB、CD中点.求证2EF<AC+BD注意 2020-05-22 …
如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.(1)若四边形AECF是平行 2020-06-13 …
关于任意四边形分为两等面积部分的问题请问在任意一个四边形中,已经给定一条过顶点的好线(好线:在任意 2020-06-13 …
八年级全等三角形在四边形ABCD中,BC大于BA,AD=CB,BD平分∠ABC,求证∠BAD+∠C 2020-08-01 …