早教吧作业答案频道 -->数学-->
如图1,在△ABC中,在BC边上取一点P,在AC边上取一点D,连AP、PD,如果△APD是等腰三角形且△ABP与△CDP相似,我们称△APD是AC边上的“等腰邻相似三角形”.(1)如图2,在△ABC中AB=AC,∠B=50&
题目详情
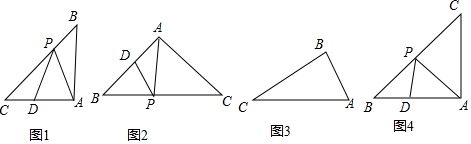
如图1,在△ABC中,在BC边上取一点P,在AC边上取一点D,连AP、PD,如果△APD是等腰三角形且△ABP与△CDP相似,我们称△APD是AC边上的“等腰邻相似三角形”.
(1)如图2,在△ABC中AB=AC,∠B=50°,△APD是AB边上的“等腰邻相似三角形”,且AD=DP,∠PAC=∠BPD,则∠PAC的度数是___;
(2)如图3,在△ABC中,∠A=2∠C,在AC边上至少存在一个“等腰邻相似△APD”,请画出一个AC边上的“等腰邻相似△APD”,并说明理由;
(3)如图4,在Rt△ABC中AB=AC=2,△APD是AB边上的“等腰邻相似三角形”求出AD长度的所有可能值.
(1)如图2,在△ABC中AB=AC,∠B=50°,△APD是AB边上的“等腰邻相似三角形”,且AD=DP,∠PAC=∠BPD,则∠PAC的度数是___;
(2)如图3,在△ABC中,∠A=2∠C,在AC边上至少存在一个“等腰邻相似△APD”,请画出一个AC边上的“等腰邻相似△APD”,并说明理由;
(3)如图4,在Rt△ABC中AB=AC=2,△APD是AB边上的“等腰邻相似三角形”求出AD长度的所有可能值.

▼优质解答
答案和解析
(1)如图2中,
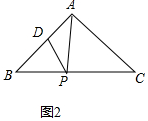
∵AB=AC,DA=DP,
∴∠B=∠C,∠DAP=∠DPA,
∵∠PAC=∠BPD,
∴∠APC=∠BDP=∠DAP+∠DPA,
∵∠APC=∠B+∠BAP,
∴∠B=∠PAB=50°,
∵∠BAC=180°-50°-50°=80°,
∴∠PAC=30°
故答案为30°.
(2)如图3中,作∠BAC的平分线AP交BC于P,作PD∥AB交AC于D,
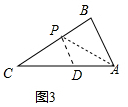
∴∠BAP=∠PAD=∠DPA,∠CPD=∠B,
∵∠CAB=2∠C,
∴∠PAD=∠C,
∴DP=DA,
∴△APD是等腰三角形且与△APB与△CDP相似.
(3)如图3′中,当DA=DP时,设∠APD=∠DAP=x,
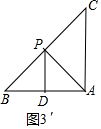
①若∠BPD=∠CAP=90°-x,∠BDP=∠CPA=2x,
∴90°-x+2x+x=180°,
∴x=45°,
∴三角形都是等腰直角三角形,易知AD=1,
②若∠PDB=∠CAP时,设∠APD=∠DAP=x,得到∠PDB=∠CAP=2x,易知x=30°,设AD=a,则AP=
a,
∵△BPD∽△CPA,
∴
=
,即
=
a,解得a=
,
如图4中,当PA=PD时,易知∠PDB是钝角,∠CAP是锐角,
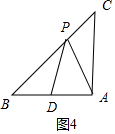
∴∠PDB=∠CPA,则△BPD≌△CPA,设AD=a,则BD=2-a,BP=2
-(2-a),AC=2,
2
-(2-a)=2,
解得a=4-2
,
如图5中,当AP=AD时,设∠APD=∠ADP=x,则∠DAP=180°-2x,易知∠PDB为钝角,∠CAP为锐角,
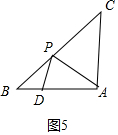
∴∠PDB=∠CAP=180°-x,∠CAP=90°-∠DAP=90°-(180°-2x)=2x-90°,
在△APC中,2x-90°+180°-x+45°=180°,解得x=45°,不可能成立.
综上所述.AD的长为1或
或4-2

∵AB=AC,DA=DP,
∴∠B=∠C,∠DAP=∠DPA,
∵∠PAC=∠BPD,
∴∠APC=∠BDP=∠DAP+∠DPA,
∵∠APC=∠B+∠BAP,
∴∠B=∠PAB=50°,
∵∠BAC=180°-50°-50°=80°,
∴∠PAC=30°
故答案为30°.
(2)如图3中,作∠BAC的平分线AP交BC于P,作PD∥AB交AC于D,

∴∠BAP=∠PAD=∠DPA,∠CPD=∠B,
∵∠CAB=2∠C,
∴∠PAD=∠C,
∴DP=DA,
∴△APD是等腰三角形且与△APB与△CDP相似.
(3)如图3′中,当DA=DP时,设∠APD=∠DAP=x,

①若∠BPD=∠CAP=90°-x,∠BDP=∠CPA=2x,
∴90°-x+2x+x=180°,
∴x=45°,
∴三角形都是等腰直角三角形,易知AD=1,
②若∠PDB=∠CAP时,设∠APD=∠DAP=x,得到∠PDB=∠CAP=2x,易知x=30°,设AD=a,则AP=
| 3 |
∵△BPD∽△CPA,
∴
| BD |
| AC |
| PD |
| PA |
| 2-a |
| 2 |
| a | ||
|
6-2
| ||
| 3 |
如图4中,当PA=PD时,易知∠PDB是钝角,∠CAP是锐角,

∴∠PDB=∠CPA,则△BPD≌△CPA,设AD=a,则BD=2-a,BP=2
| 2 |
2
| 2 |
解得a=4-2
| 2 |
如图5中,当AP=AD时,设∠APD=∠ADP=x,则∠DAP=180°-2x,易知∠PDB为钝角,∠CAP为锐角,

∴∠PDB=∠CAP=180°-x,∠CAP=90°-∠DAP=90°-(180°-2x)=2x-90°,
在△APC中,2x-90°+180°-x+45°=180°,解得x=45°,不可能成立.
综上所述.AD的长为1或
6-2
| ||
| 3 |
作业帮用户
2016-11-21
|
看了 如图1,在△ABC中,在BC...的网友还看了以下:
英语翻译四边形ABCD有外接圆的充要条件是$S=sqrt((p-a)*(p-b)*(p-c)*(p- 2020-03-31 …
如图A、B、C是一条公路上的三个村庄,A、B间的路程为100m,A、C间设一车站P,设PC为xm. 2020-05-16 …
物理题``关于变阻器``已知RAB=50欧,RAP=20欧,则RCD=欧,RAD=欧,RBD=欧. 2020-06-02 …
已知互不相等的正数a,b,c,d,p,q满足a,c,b,d成等差数列,a,p,b,q成等比数列,则 2020-06-12 …
求证:四边形ABCD有外接圆的充要条件是S=√((p-a)*(p-b)*(p-c)*(p-d))其 2020-06-23 …
一条线段上有9个点包括端点,从左至右依次为A,M,C.P,D,Q,E,N,B,且AC:CD:DE: 2020-07-30 …
关于海伦公式的推论三角形的是S=SQR[P(P-A)(P-B)(P-C)]圆内接四边形是S=SQR 2020-07-30 …
设A是n阶实对称矩阵,P是n阶可逆矩阵.已知n维列向量α是A的属于特征值λ的特征向量,则矩阵(P-1 2020-11-02 …
S²=(p-a)(p-b)(p-c)(p-d),其中p=½(a+b+c+d)这个公式怎么用S²=(p 2020-11-07 …
设M={X|f(x)=0}≠Φ,N={x|g(x)=0}≠Φ,P={X|f(x)g(x)=0}≠Φ, 2020-12-25 …
 扫描下载二维码
扫描下载二维码