早教吧作业答案频道 -->数学-->
如图,抛物线y=12x2-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.(1)直接写出A、B、C的坐标;(2)求抛物线y=12x2-x-4的对称轴和顶点坐
题目详情
如图,抛物线y=
x2-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
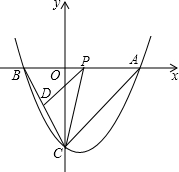
(1)直接写出A、B、C的坐标;
(2)求抛物线y=
x2-x-4的对称轴和顶点坐标;
(3)求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.
| 1 |
| 2 |

(1)直接写出A、B、C的坐标;
(2)求抛物线y=
| 1 |
| 2 |
(3)求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.
▼优质解答
答案和解析
(1)A(4,0)、B(-2,0)、C(0,-4).
(2)抛物线:y=
x2-x-4=
(x-1)2-
,
∴抛物线的对称轴是直线x=1,顶点坐标是(1,-
).
(3)设P(x,0)(-2<x<4),
∵PD∥AC,
∴
=
,
解得:PD=
(x+2),
∵C到PD的距离(即P到AC的距离):d=PA×sin450=
(4-x),
∴△PCD的面积S=
×PD×d=
(x+2)(4-x)=-
x2+
x+
,
∴S=-
(x-1)2+3,
∴△PCD面积的最大值为3,
当△PCD的面积取最大值时,x=1,PA=4-x=3,PD=
(x+2)=2
,
因为PA≠PD,所以以PA、PD为邻边的平行四边形不是菱形.
(2)抛物线:y=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴抛物线的对称轴是直线x=1,顶点坐标是(1,-
| 9 |
| 2 |
(3)设P(x,0)(-2<x<4),
∵PD∥AC,
∴
| PD |
| AC |
| BP |
| AB |
解得:PD=
2
| ||
| 3 |
∵C到PD的距离(即P到AC的距离):d=PA×sin450=
| ||
| 2 |
∴△PCD的面积S=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
∴S=-
| 1 |
| 3 |
∴△PCD面积的最大值为3,
当△PCD的面积取最大值时,x=1,PA=4-x=3,PD=
2
| ||
| 3 |
| 2 |
因为PA≠PD,所以以PA、PD为邻边的平行四边形不是菱形.
看了 如图,抛物线y=12x2-x...的网友还看了以下:
在图中,平行线间的三个图形,它们的面积相比()A.a图形最大B.b图形最大C.c图形最大D.三个图 2020-05-02 …
如图,直线AB上有5个点A,B,C,D,E.1.图中一共有多少条射线?2.图中一共有多少条线段?3 2020-06-02 …
如图,∠BAC=60°,∠CDE=120°,AB=AC,DC=DE,连接BE,P为BE的中点.(1 2020-06-15 …
汽车通过如图所示的一段路面,其中AB、CD分别为水平路面,BC为一段斜坡,全程路面的材质相同,各路 2020-06-15 …
(1)如图1所示,小球沿光滑的线路由A经B、C到D,已知弧AB、弧CD和线段BC三段长度相等,A、 2020-06-22 …
如图所示,三段材质、粗细完全一样的轻绳,其中AO与BO垂直,BO与竖直方向的夹角为θ,当不断增大重 2020-07-31 …
把三张形状大小相同但是画面不相同的风景图片都平均剪成三段,然后将上、中、下三段分别混合洗匀,再从三 2020-08-01 …
把三张形状大小相同但是画面不相同的风景图片都平均剪成三段,然后将上、中、下三段分别混合洗匀,再从三 2020-08-01 …
把三张形状大小相同但是画面不相同的风景图片都平均剪成三段,然后将上、中、下三段分别混合洗匀,再从三 2020-08-01 …
第一个图形是一条线段第二个图形是三条线段第三个图形是六条线段你发现了什么规律?第100个图形是几条线 2020-11-27 …