早教吧作业答案频道 -->数学-->
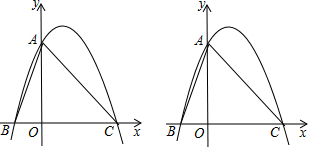
如图,抛物线y=-12x2+bx+3,与x轴交于点B(-2,0)和C,与y轴交于点A,点M在y轴上.(1)求抛物线的解析式;(2)连结BM并延长,交抛物线于D,过点D作DE⊥x轴于E.当以B、D、E为顶点的三角形
题目详情
如图,抛物线y=-
x2+bx+3,与x轴交于点B(-2,0)和C,与y轴交于点A,点M在y轴上.
(1)求抛物线的解析式;
(2)连结BM并延长,交抛物线于D,过点D作DE⊥x轴于E.当以B、D、E为顶点的三角形与△AOC相似时,求点M的坐标;
(3)连结BM,当∠OMB+∠OAB=∠ACO时,求AM的长.
| 1 |
| 2 |
(1)求抛物线的解析式;
(2)连结BM并延长,交抛物线于D,过点D作DE⊥x轴于E.当以B、D、E为顶点的三角形与△AOC相似时,求点M的坐标;
(3)连结BM,当∠OMB+∠OAB=∠ACO时,求AM的长.

▼优质解答
答案和解析
(1)将点B(-2,0)代入抛物线的解析式y=-
x2+bx+3得
-
×(-2)2-2b+3=0,
∴b=
,
∴抛物线的解析式为y=-
x2+
x+3.
(2)如图1中,
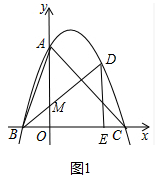
∵抛物线的解析式为y=-
x2+
x+3,与x轴交于B(-2,0),A(3,0),C(0,3),
∴OA=OC,
∴△AOC是等腰直角三角形,
∵OM∥DE,
∴△BMO∽△BDE,
∵要使B、D、E为顶点的三角形与△AOC相似,
∴只要△BOM∽△AOC,设M(0,m),
∴
=
,
∴
=
,
∴m=±2,
∴点M的坐标为(2,0)或(-2,0).
(3)如图2中,作AG⊥AC交x轴于G,BF⊥AG于F.
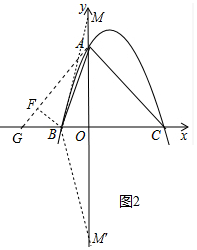
∵OA=OC,∠AOC=∠GAC=90°,
∴∠OAC=∠ACO=∠OAG=45°,
∵∠OMB+∠OAB=∠ACO=45°,
∴∠FAB=∠OMB,设M(n,0),
∵∠AFB=∠BOM=90°,
∴△AFB∽△MOB,
∴
=
,∵FB=
,AF=
,OB=2,
∴
=
,
∴n=±10,
∴点M的坐标为(0,10)或(0,-10).
| 1 |
| 2 |
-
| 1 |
| 2 |
∴b=
| 1 |
| 2 |
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图1中,

∵抛物线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=OC,
∴△AOC是等腰直角三角形,
∵OM∥DE,
∴△BMO∽△BDE,
∵要使B、D、E为顶点的三角形与△AOC相似,
∴只要△BOM∽△AOC,设M(0,m),
∴
| OM |
| OB |
| OA |
| OC |
∴
| |m| |
| 2 |
| 3 |
| 3 |
∴m=±2,
∴点M的坐标为(2,0)或(-2,0).
(3)如图2中,作AG⊥AC交x轴于G,BF⊥AG于F.

∵OA=OC,∠AOC=∠GAC=90°,
∴∠OAC=∠ACO=∠OAG=45°,
∵∠OMB+∠OAB=∠ACO=45°,
∴∠FAB=∠OMB,设M(n,0),
∵∠AFB=∠BOM=90°,
∴△AFB∽△MOB,
∴
| OM |
| AF |
| OB |
| FB |
| ||
| 2 |
5
| ||
| 2 |
∴
| |n| | ||||
|
| 2 | ||||
|
∴n=±10,
∴点M的坐标为(0,10)或(0,-10).
看了 如图,抛物线y=-12x2+...的网友还看了以下:
在直角坐标系中,已知线段AB,点A的坐标为(1,-2),点B的坐标为(3,0),如图1所示.(1) 2020-06-14 …
如图,在△ABC中,∠A=90°,∠B=60°,AB=3,点D从点A以每秒1个单位长度的速度向点B 2020-07-20 …
(2013•昭通)已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD 2020-07-21 …
已知三角形abc为等边三角形,点D,F分别在边BC,AC上,且DF//AB,过点A平行于BC的直线 2020-07-22 …
已知三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F求证三角形ABE全已知 2020-08-01 …
如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D 2020-08-02 …
如图,三角形ABC为等边三角形.点D为BC边上一动点(不与BC重合),∠DAE=60°,过点B作B 2020-08-03 …
三角形ABC是等边三角形,点D是射线BC上的一个动点(D不与B、C重合)三角形ADE是以AD为边的 2020-08-03 …
已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF 2020-08-03 …
大雾形成的条件中与深秋初冬季节相关的是()A.昼夜温差较小,水汽易凝结形成B.昼夜温差较小,水汽不易 2020-12-07 …