早教吧作业答案频道 -->数学-->
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为3的正三角形,AC与BD交于点O,点M是PB的中点.(1)求证:OM∥平面PAD;(2)求三棱锥M-PCD的体积.
题目详情
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为
的正三角形,AC与BD交于点O,点M是PB的中点.
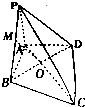
(1)求证:OM∥平面PAD;
(2)求三棱锥M-PCD的体积.
| 3 |

(1)求证:OM∥平面PAD;
(2)求三棱锥M-PCD的体积.
▼优质解答
答案和解析
(1)∵△BCD是正三角形,∴BC=CD,
∵∠ABC=∠ADC=90°,AC=AC,
∴△ABC≌△ADC,
∴∠BCO=∠DCO,
∴O是BD的中点,又M是PB的中点,
∴OM∥PD,又OM⊄平面PAD,PD⊂平面PAD,
∴OM∥平面PAD.
(2)∵△BCD是边长为
的正三角形,
∴∠CBD=∠CDB=60°,BD=
,OC=
.
∵∠ABC=∠ADC=90°,
∴∠OBA=∠ODA=30°,∴∠BAD=120°,
∴PA=AD=1.
∵OM∥PD,∴OM∥平面PCD,
∴VM-PCD=VO-PCD=VP-OCD=
S△OCD•PA=
×
×
×
×1=
.
∵∠ABC=∠ADC=90°,AC=AC,
∴△ABC≌△ADC,
∴∠BCO=∠DCO,
∴O是BD的中点,又M是PB的中点,
∴OM∥PD,又OM⊄平面PAD,PD⊂平面PAD,
∴OM∥平面PAD.
(2)∵△BCD是边长为
| 3 |
∴∠CBD=∠CDB=60°,BD=
| 3 |
| 3 |
| 2 |
∵∠ABC=∠ADC=90°,
∴∠OBA=∠ODA=30°,∴∠BAD=120°,
∴PA=AD=1.
∵OM∥PD,∴OM∥平面PCD,
∴VM-PCD=VO-PCD=VP-OCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 8 |
看了 如图,在四棱锥P-ABCD中...的网友还看了以下:
神舟十号飞船于2013年6月11日17时38分在甘肃酒泉(39.44°N,98.31°E)成功发射 2020-05-13 …
已知如图,数轴上A、B、C、D四点对应的有理数分别是整数a、b、c、d,且c-2a=7,则原点应是 2020-05-15 …
如图是人体心脏结构示意图,请据图回答下列问题(1)在心脏的四个腔中,A是,B是,C是,D是其中心脏 2020-06-13 …
如图,EC⊥CF于C,点A在CE上,点B在CF上,BD平分∠CBA,AG平分∠EAB,且直线AG交 2020-06-27 …
数学概率之独立事件已知A与B独立,C包含于B,而D包含于A,还有E也包含于A.下面问:1、A与C是 2020-07-30 …
4.已知A、B、C、D有下列关系,请推出A与B、B与D、A与D的外延关系,写出推导过程,并将A、B、 2020-11-07 …
如图是蜡烛在平面镜成像的光路图.都能看到蜡烛S在平面镜中的像的区域是()A.a与b两条光线之间B.a 2020-12-05 …
如图所示,若在a、b、c、d四个接线柱之间连接,要使灯L1、L2组成并联电路,则下列连接方法中不正确 2020-12-05 …
假如“神九”于7月份某日上天与“天宫一号”相会,到进地球行到图2中的()A、a与b之间B、b与c之间 2020-12-09 …
第十一届全运会于2009.10.11~10.23在山东济南(117°02′E,36°40′N)隆重召 2020-12-17 …