早教吧作业答案频道 -->物理-->
如图所示,在竖直平面内有足够长的平行金属导轨MN、PQ,其间距为L=2m,在N、Q之间连接由阻值为R=0.8Ω的电阻,一匀强磁场与导轨平面垂直,磁感应强度为B0,现有一细线绕过光滑的轻质定滑
题目详情
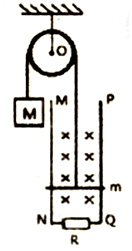
如图所示,在竖直平面内有足够长的平行金属导轨MN、PQ,其间距为L=2m,在N、Q之间连接由阻值为R=0.8Ω的电阻,一匀强磁场与导轨平面垂直,磁感应强度为B0,现有一细线绕过光滑的轻质定滑轮,一端系一质量为M=3kg的重物,另一端与质量为m=1kg的金属杆相连,金属杆接入两导轨间的电阻为r=0.2Ω,开始时金属杆置于导轨下端NQ处,将重物由静止释放,当重物下降h=5m时恰好达到温度速度v而匀速下降,已知v=5m/s,且运动过程中金属杆始终与导轨垂直且接触良好,不计一切摩擦和导轨电阻,重力加速度g=10m/s2,求:
(1)匀强磁场的磁感应强度B0;
(2)重物从释放到下降h的过程中,电阻R中产生的热量QR.
(3)设重物下降h时的时刻t=0,若从t=0开始,磁场的磁感应强度B逐渐减小,且金属杆中始终不产生感应电流,试写出B随时间t变化关系.

(1)匀强磁场的磁感应强度B0;
(2)重物从释放到下降h的过程中,电阻R中产生的热量QR.
(3)设重物下降h时的时刻t=0,若从t=0开始,磁场的磁感应强度B逐渐减小,且金属杆中始终不产生感应电流,试写出B随时间t变化关系.
▼优质解答
答案和解析
(1)设细线的拉力为T,匀速运动时通过金属棒的电流为I,
对金属棒:FT=F安+mg,
对M有:Mg=FT,
其中:F安=B0IL,E=B0Lv,E=I(R+r),
故B0=1T;
(2)设电路中产生的总焦耳热为Q,由能量守恒定律得:
(M-m)gh=
Mv2+
mv2+Q,
解得:Q=50J;
根据串联电路特点,电阻R中产生的焦耳热:QR=
Q,
解得:QR=40J;
(3)金属杆中不产生感应电流是回路的磁通量不变,所以:B0hL=B(h+x)L,
其中:x=vt+
at2,
根据牛顿第二定律,有:Mg-mg=(M+m)a,
解得:B=
;
答:(1)匀强磁场的磁感应强度B0为1T;
(2)重物从释放到下降h的过程中,电阻R中产生的热量QR为40J;
(3)B随时间t变化关系为B=
.
对金属棒:FT=F安+mg,
对M有:Mg=FT,
其中:F安=B0IL,E=B0Lv,E=I(R+r),
故B0=1T;
(2)设电路中产生的总焦耳热为Q,由能量守恒定律得:
(M-m)gh=
| 1 |
| 2 |
| 1 |
| 2 |
解得:Q=50J;
根据串联电路特点,电阻R中产生的焦耳热:QR=
| R |
| R+r |
解得:QR=40J;
(3)金属杆中不产生感应电流是回路的磁通量不变,所以:B0hL=B(h+x)L,
其中:x=vt+
| 1 |
| 2 |
根据牛顿第二定律,有:Mg-mg=(M+m)a,
解得:B=
| 2 |
| 2+2t+t2 |
答:(1)匀强磁场的磁感应强度B0为1T;
(2)重物从释放到下降h的过程中,电阻R中产生的热量QR为40J;
(3)B随时间t变化关系为B=
| 2 |
| 2+2t+t2 |
看了 如图所示,在竖直平面内有足够...的网友还看了以下:
如图所示,电阻不计的平行金属导轨与水平面成θ角,导轨与定值电阻R1和R2相连,匀强磁场垂直穿过导轨 2020-06-08 …
(2013•陕西三模)如图所示,平行金属导轨与水平面成α角,导轨与固定电阻R1和R2相连,匀强磁场 2020-07-29 …
如图所示,水平放置的平行金属导轨宽度为d=1m,导轨间接有一个阻值为R=2Ω的电阻,一质量为m=1k 2020-12-17 …
如图所示,空间有磁感应强度为B、方向竖直向上的匀强磁场,两平行光滑金属导轨水平放置,其电阻不计、间距 2020-12-31 …
如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P 2020-12-31 …
如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P 2020-12-31 …
如图所示,水平面上有两根相距1m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间 2020-12-31 …
如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P 2020-12-31 …
如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P 2020-12-31 …
如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P 2020-12-31 …