早教吧作业答案频道 -->数学-->
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.
题目详情
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
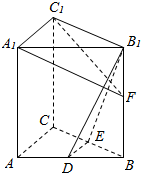
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.

(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
▼优质解答
答案和解析
(1)∵D,E分别为AB,BC的中点,
∴DE为△ABC的中位线,
∴DE∥AC,
∵ABC-A1B1C1为棱柱,
∴AC∥A1C1,
∴DE∥A1C1,
∵A1C1⊂平面A1C1F,且DE⊄平面A1C1F,
∴DE∥A1C1F;
(2)∵ABC-A1B1C1为直棱柱,
∴AA1⊥平面A1B1C1,
∴AA1⊥A1C1,
又∵A1C1⊥A1B1,且AA1∩A1B1=A1,AA1、A1B1⊂平面AA1B1B,
∴A1C1⊥平面AA1B1B,
∵DE∥A1C1,
∴DE⊥平面AA1B1B,
又∵A1F⊂平面AA1B1B,
∴DE⊥A1F,
又∵A1F⊥B1D,DE∩B1D=D,且DE、B1D⊂平面B1DE,
∴A1F⊥平面B1DE,
又∵A1F⊂平面A1C1F,
∴平面B1DE⊥平面A1C1F.
∴DE为△ABC的中位线,
∴DE∥AC,
∵ABC-A1B1C1为棱柱,
∴AC∥A1C1,
∴DE∥A1C1,
∵A1C1⊂平面A1C1F,且DE⊄平面A1C1F,
∴DE∥A1C1F;
(2)∵ABC-A1B1C1为直棱柱,
∴AA1⊥平面A1B1C1,
∴AA1⊥A1C1,
又∵A1C1⊥A1B1,且AA1∩A1B1=A1,AA1、A1B1⊂平面AA1B1B,
∴A1C1⊥平面AA1B1B,
∵DE∥A1C1,
∴DE⊥平面AA1B1B,
又∵A1F⊂平面AA1B1B,
∴DE⊥A1F,
又∵A1F⊥B1D,DE∩B1D=D,且DE、B1D⊂平面B1DE,
∴A1F⊥平面B1DE,
又∵A1F⊂平面A1C1F,
∴平面B1DE⊥平面A1C1F.
看了 如图,在直三棱柱ABC-A1...的网友还看了以下:
如图,已知直线a‖b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为如图,已 2020-05-16 …
如果直线a、b是异面直线,点A、C在直线a上,B、D在直线b上,那么直线AB和CD一定是()A.平 2020-06-03 …
在同一平面内,过一点可能有两条以上的直线与已知直线平行吗?任意画一条直线a,在直线外取点P,并过点 2020-06-06 …
根据下列语句画出图形1.直线l与直线m相交于点A,直线m与直线n相交于点C,直线你与直线l相交于点 2020-06-12 …
(1)画一点P,过点P画直线AB,在直线AB外画一点Q.(2)点A在直线点l上,点B和点C都(1) 2020-07-20 …
a,b是异面直线,()A,若P为不在a,b上的一点,则过点p有且只有一个平面与a,b平行B,过直线 2020-07-22 …
如果直线a、b是异面直线,点A、C在直线a上,B、D在直线b上,那么直线AB和CD一定是()A.平 2020-07-25 …
定义映射:f:A(x,y)→B(x+根号3y,根号3-y),是否存在这样的直线l:若点A在直线l上 2020-07-30 …
如果直线a、b是异面直线,点A、C在直线a上,B、D在直线b上,那么直线AB和CD一定是()A.平 2020-08-02 …
已知直线a和b是两条异面直线,点A、C在直线a上,点B、D在直线b上,且A、B、C、D是不同的四点 2020-08-02 …