早教吧作业答案频道 -->数学-->
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=k2x的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+12n=0;③S
题目详情
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=
的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+
n=0;③S△AOP=S△BOQ;④不等式k1x+b>
的解集是x<-2或0<x<1,其中正确的结论的序号是___.
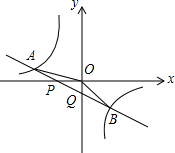
| k2 |
| x |
| 1 |
| 2 |
| k2 |
| x |

▼优质解答
答案和解析
由图象知,k1<0,k2<0,
∴k1k2>0,故①错误;
把A(-2,m)、B(1,n)代入y=
中得-2m=n,
∴m+
n=0,故②正确;
把A(-2,m)、B(1,n)代入y=k1x+b得
,
∴
,
∵-2m=n,
∴y=-mx-m,
∴P(-1,0),Q(0,-m),
∴OP=1,OQ=m,
∴S△AOP=
m,S△BOQ=
m,
∴S△AOP=S△BOQ;故③正确;
由图象知不等式k1x+b>
的解集是x<-2或0<x<1,故④正确;
故答案为:②③④.
∴k1k2>0,故①错误;
把A(-2,m)、B(1,n)代入y=
| k2 |
| x |
∴m+
| 1 |
| 2 |
把A(-2,m)、B(1,n)代入y=k1x+b得
|
∴
|
∵-2m=n,
∴y=-mx-m,
∴P(-1,0),Q(0,-m),
∴OP=1,OQ=m,
∴S△AOP=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AOP=S△BOQ;故③正确;
由图象知不等式k1x+b>
| k2 |
| x |
故答案为:②③④.
看了 如图,已知直线y=k1x+b...的网友还看了以下:
判断(0,0)是不是二元函数极值点已知二元函数f(x,y)在点(0,0)某邻域内连续,且当x,y趋 2020-05-23 …
设f(x,y)在点(0,0)处连续,且lim(x,y)→(0,0)f(x,y)−1ex2+y2−1 2020-06-12 …
求e^(2x+3y)关于x和y的从0到1的二重积分计算,时间久了忘了怎么算了, 2020-07-08 …
以下多元函数极限是否存在?为什么?(1)f(x,y)=[(2+x)ln(1+xy)]/(xy),( 2020-07-09 …
f(x,y)=xy/(x^2+y^2),(x,y)≠(0,0);其他=0.是讨论极限limf(x, 2020-07-16 …
已知x、y、z满足2x-y-2z-6=0,已知x、y、z满足2x-y-2z-6=0,x2+y2+z2 2020-10-31 …
看不懂下题过程,从“x,y是实数”开始,求解y+x-4=2√(x^+9),平方得x^+2(y-4)x 2020-10-31 …
已知道2[√X+√(Y-1)+√(Z-2)]=X+Y+Z,求X,Y,Z2[√X+√(Y-1)+√(Z 2020-11-01 …
已知x,y为有理数,且x≠0,y≠0,求|x|/x+|y|/y的值.①已知x,y,z为有理数,且x≠ 2020-12-31 …
对于lim(x→0,y→0)sinxy/y为什么不能用等价代换使原式=lim(x→0,对于lim(x 2021-01-07 …