在矩形ABCD中，AB=6，AD=8，P是BC边上一个动点（不与点B重合）．设PA=x，点D到PA的距离为y，求y与x之间的函数表达式，并求出自变量x的取值范围．

Question

在矩形ABCD中，AB=6，AD=8，P是BC边上一个动点（不与点B重合）．设PA=x，点D到PA的距离为y，求y与x之间的函数表达式，并求出自变量x的取值范围．
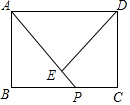在矩形ABCD中，AB=6，AD=8，P是BC边上一个动点（不与点B重合）．设PA=x，点D到PA的距离为y，求y与x之间的函数表达式，并求出自变量x的取值范围．

Answer 1

∵在矩形ABCD中，
∴AD∥BC，
∴∠DAE=∠APB，
∵∠B=∠AED=90°，
∴△ABP∽△DEA，
∴(DE)/(AB)=(AD)/(AP)，
∴(y)/(6)=(8)/(x)，
故y=(48)/(x)，
∵AB=6，AD=8，
∴矩形对角线AC=√(62+82)=10，
∴x的取值范围是：6<x≤10． (DE)/(AB)DEABDEDEDEABABAB=(AD)/(AP)，
∴(y)/(6)=(8)/(x)，
故y=(48)/(x)，
∵AB=6，AD=8，
∴矩形对角线AC=√(62+82)=10，
∴x的取值范围是：6<x≤10． (AD)/(AP)ADAPADADADAPAPAP，
∴(y)/(6)=(8)/(x)，
故y=(48)/(x)，
∵AB=6，AD=8，
∴矩形对角线AC=√(62+82)=10，
∴x的取值范围是：6<x≤10． (y)/(6)y6yyy666=(8)/(x)，
故y=(48)/(x)，
∵AB=6，AD=8，
∴矩形对角线AC=√(62+82)=10，
∴x的取值范围是：6<x≤10． (8)/(x)8x888xxx，
故y=(48)/(x)，
∵AB=6，AD=8，
∴矩形对角线AC=√(62+82)=10，
∴x的取值范围是：6<x≤10． (48)/(x)48x484848xxx，
∵AB=6，AD=8，
∴矩形对角线AC=√(62+82)=10，
∴x的取值范围是：6<x≤10． √(62+82)

62+82

62+82

62+8262+822+822=10，
∴x的取值范围是：6