早教吧作业答案频道 -->数学-->
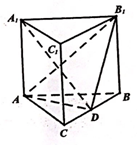
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为π3,点D线段BC的中点.(1)若AB=AC,求证:平面BB1C1C⊥平面AB1D;(2)当三棱柱ABC-A1B1C1的体积最大时,求直线A1D与平面AB1D所
题目详情
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为
,点D线段BC的中点.
(1)若AB=AC,求证:平面BB1C1C⊥平面AB1D;
(2)当三棱柱ABC-A1B1C1的体积最大时,求直线A1D与平面AB1D所成角θ的正弦值.
| π |
| 3 |

(1)若AB=AC,求证:平面BB1C1C⊥平面AB1D;
(2)当三棱柱ABC-A1B1C1的体积最大时,求直线A1D与平面AB1D所成角θ的正弦值.
▼优质解答
答案和解析
(1)证明:由题意,∠ACB=
,AB=AC,
∴△ABC为正三角形,∴AD⊥BC,AD⊥CC1,
∴AD⊥平面BB1C1C,
∵AD⊂平面AB1D,
∴平面BB1C1C⊥平面AB1D;
(2) 当三棱柱ABC-A1B1C1的底面积最大时,体积最大,
∵4=AB2=AC2+BC2-2AC•BC•
≥AC•BC-AC•BC=AC•BC,
∴当AC=BC,三角形ABC为正三角形时面积取最大值,
设A1到平面AB1D的距离为d,则由等体积可得
S△AB1D•d=
•
•AD•DB1•d=
,
∴d=
,
∴sinθ=
=
=
.
| π |
| 3 |
∴△ABC为正三角形,∴AD⊥BC,AD⊥CC1,
∴AD⊥平面BB1C1C,
∵AD⊂平面AB1D,
∴平面BB1C1C⊥平面AB1D;
(2) 当三棱柱ABC-A1B1C1的底面积最大时,体积最大,
∵4=AB2=AC2+BC2-2AC•BC•
| 1 |
| 2 |
∴当AC=BC,三角形ABC为正三角形时面积取最大值,
设A1到平面AB1D的距离为d,则由等体积可得
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
∴d=
| 2 | ||
|
∴sinθ=
| d |
| A1D |
| ||||
|
2
| ||
| 35 |
看了 如图,已知在直三棱柱ABC-...的网友还看了以下:
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线 2020-04-26 …
在平面坐标系中 抛物线的解析式是y=1/4xx+1,点c的坐标为(-4.0),平行四边形oabc的 2020-05-16 …
在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为4,且 2020-05-16 …
已知二面角α-PQ-β,为60°,点A和B分别在平面α和平面β内,点C在棱PQ上角ACP=角BCP 2020-05-16 …
1、数轴上的点A、点B分别表示的数是-2和1,点C、点D(点C在点D的左边)将线段AB分成三等份, 2020-05-22 …
已知直线l1:k1x-5与y轴交与点A,l2:y2=k2x+7与y轴交与点B,两直线交与点C,点C 2020-06-14 …
已只直线y=1/2x与双曲线y=k/x(k>0)交A,B2点,且A的横坐标为4求1k的值2若双曲线 2020-07-12 …
如图,物体以4米每秒的初速度自斜面低端A点,滑丄光滑的斜面,途径斜面中点C,到达最高点B.一直在A 2020-07-26 …
如图已知二面角α-PQ-β为60°点A和点B分别在平面α和平面β内点C在棱PQ上∠ACP=∠BCP 2020-07-31 …
一张三角形纸,不用任何工具,比较,证明AB与AC长短三角形三点,下面2点是B,C上面1点是A三角形三 2020-12-14 …