早教吧作业答案频道 -->数学-->
从空间中一点P引三条射线PA,PB,PC,且三条射线两两成60°角,则二面角A-PB-C的平面角的余弦值是()A.B.C.D.
题目详情
从空间中一点P引三条射线PA,PB,PC,且三条射线两两成60°角,则二面角A-PB-C的平面角的余弦值是( )
A.
B.
C.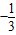
D.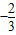
A.

B.

C.
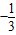
D.
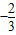
▼优质解答
答案和解析
分析:
在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,连接AC在△ACM中,作AN垂直于CM于点N,∠AMN就是二面角A-PB-C的平面角,解三角形AMN,即可得到二面角A-PB-C的余弦.
在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,所以∠AMC就是二面角A-PB-C的平面角,连接AC,由图可得,在直角△PAM中,∠APM=60°,令PM=a,则AP=2a,AM=a,同理,在直角△PCM中,∠CPM=60°,令PM=a,则CP=2a CM=a.因为∠APC=60°,PA=PC=2a,所以△PAC为等边三角形,即AC=2a.在△ACM中,作AN垂直于CM于点N,令MN=b,CN=a-b,AN=x,由勾股定理可得,在△AMN中有:( a)2-x2=b2;在△ACN中有:(2a)2-x2=( a-b)2,联合两式消去x整理的,a=b,即 =,=,所以二面角A-PB-C的余弦值是 .故选A.
点评:
本题考查的知识点是二面角的平面角及求法,其中作出二面角的平面角是解答本题的关键.
分析:
在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,连接AC在△ACM中,作AN垂直于CM于点N,∠AMN就是二面角A-PB-C的平面角,解三角形AMN,即可得到二面角A-PB-C的余弦.
在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,所以∠AMC就是二面角A-PB-C的平面角,连接AC,由图可得,在直角△PAM中,∠APM=60°,令PM=a,则AP=2a,AM=a,同理,在直角△PCM中,∠CPM=60°,令PM=a,则CP=2a CM=a.因为∠APC=60°,PA=PC=2a,所以△PAC为等边三角形,即AC=2a.在△ACM中,作AN垂直于CM于点N,令MN=b,CN=a-b,AN=x,由勾股定理可得,在△AMN中有:( a)2-x2=b2;在△ACN中有:(2a)2-x2=( a-b)2,联合两式消去x整理的,a=b,即 =,=,所以二面角A-PB-C的余弦值是 .故选A.
点评:
本题考查的知识点是二面角的平面角及求法,其中作出二面角的平面角是解答本题的关键.
看了 从空间中一点P引三条射线PA...的网友还看了以下:
关于余式定理的一道题设a、b、c是三个不同的实数,P(x)是实系数多项式.已知(1)P(x)除以( 2020-05-16 …
下列反射中,属于非条件反射的是、、、属于条件反射的是、、A.眨眼反射B.望梅止渴C.谈虎色变D,排 2020-06-28 …
如图所示,矩形区域ABCD内存在竖直向下的匀强电场,两个带正电的粒子a和b以相同的水平速度由顶点A 2020-07-10 …
该图为大气受热过程示意图,读图完成问题。小题1:图中A、C、D分别代表的是A.大气逆辐射、太阳辐射 2020-07-12 …
已知直二面角α-CD-β,A∈α,B∈β.AB长为2l,AB与α成45°角,与β成30°角,A、B 2020-08-02 …
选择与填空1.利用微粒说,,上遇到了困难.A.光的反射现象,光的干涉和折射;B.光的折射现象,光的干 2020-11-16 …
A、B、C、D、E五人一同参加飞镖比赛,其中只有一人射中飞镖盘中心,但不知是何人所射.A说:“不是我 2020-11-30 …
A.惟余:只剩下秦皇:指秦始皇嬴政射雕:比喻善射B.留滞:停留不流通风流人物:指建功立业的英雄人物宋 2020-12-16 …
阅读图,回答23~24题.23.图中A、B、C三个箭头所表示的辐射依次是()24.大气主要的直接热源 2020-12-18 …
下列属于非条件反射的是()A.婴儿的吮吸反射B.望梅止渴C.寒冷打冷颤D.杯弓蛇影,心有余悸 2021-01-01 …