早教吧作业答案频道 -->数学-->
如图,在Rt△AOB中,∠OAB=π6,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角,动点D在斜边AB上.(Ⅰ)求证:平面COD⊥平面AOB;(Ⅱ)求CD与平面AOB所成角
题目详情
如图,在Rt△AOB中,∠OAB=
,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角,动点D在斜边AB上.
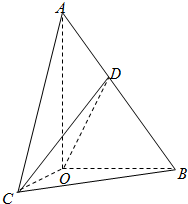
(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)求CD与平面AOB所成角的正弦的最大值.
| π |
| 6 |

(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)求CD与平面AOB所成角的正弦的最大值.
▼优质解答
答案和解析
(I)证明:由题意,CO⊥AO,BO⊥AO,
∴∠BOC是二面角B-AO-C的平面角;
又∵二面角B-AO-C是直二面角,
∴CO⊥BO,
又∵AO∩BO=O,∴CO⊥平面AOB,
又CO⊂平面COD,∴平面COD⊥平面AOB;
(II)由(I)知,CO⊥平面AOB,
∴∠CDO是CD与平面AOB所成的角;
在Rt△CDO中,CO=BO=ABsin
=4×
=2,
∴sin∠CDO=
=
;
当CD最小时,sin∠CDO最大,
此时OD⊥AB,垂足为D,
由三角形的面积相等,得
CD•AB=
BC•
,
解得CD=
=
,
∴CD与平面AOB所成角的正弦的最大值为
=
.
∴∠BOC是二面角B-AO-C的平面角;
又∵二面角B-AO-C是直二面角,
∴CO⊥BO,
又∵AO∩BO=O,∴CO⊥平面AOB,
又CO⊂平面COD,∴平面COD⊥平面AOB;
(II)由(I)知,CO⊥平面AOB,
∴∠CDO是CD与平面AOB所成的角;
在Rt△CDO中,CO=BO=ABsin
| π |
| 6 |
| 1 |
| 2 |
∴sin∠CDO=
| CO |
| CD |
| 2 |
| CD |
当CD最小时,sin∠CDO最大,
此时OD⊥AB,垂足为D,
由三角形的面积相等,得
| 1 |
| 2 |
| 1 |
| 2 |
AB2-(
|
解得CD=
2
| ||||||
| 4 |
| 7 |
∴CD与平面AOB所成角的正弦的最大值为
| 2 | ||
|
2
| ||
| 7 |
看了 如图,在Rt△AOB中,∠O...的网友还看了以下:
关于斜面的问题!不是说当光滑程度一定时,当斜面的倾斜程度不同时,斜面倾斜程度越大,机械效率越高,越 2020-05-16 …
如图所示,小车上固定着光滑的斜面,斜面倾角为θ,小车以恒定的加速度向前运动,有一物体放于斜面上,相 2020-06-18 …
物块A放置在与水平地面成30°角倾斜的木板上时,刚好可以沿斜面匀速下滑;若该木板与水平面成60°角 2020-06-22 …
已知PO是平面α的垂线,O为垂足,PO=6,PA,PB,PC是平面α的斜线,A,B,C是斜足已知P 2020-07-30 …
所谓的几何体轴截面面积用的是不是斜高,还有其表面及,侧面积,底面积用的是不是斜高所谓的几何体,如棱 2020-07-31 …
在平面斜角坐标系的题、急!在平面斜角坐标系xoy中,角xoy=60度.平面上任一点P在斜坐标系中的 2020-08-02 …
如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0 2020-12-20 …
如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0 2020-12-20 …
如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0 2020-12-20 …
如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5cm的A点由静止释放,同时小球乙自C点以速度v0 2020-12-20 …