早教吧作业答案频道 -->数学-->
如图,在三棱锥P-ABC中,AC=BC=2,AP=BP=AB,BC⊥平面PAC.(Ⅰ)求证:PC⊥AB;(Ⅱ)求三棱锥P-ABC的体积.(Ⅲ)(理科做,文科不做)求二面角B-AP-C的正弦值.
题目详情
如图,在三棱锥P-ABC中,AC=BC=2,AP=BP=AB,BC⊥平面PAC.
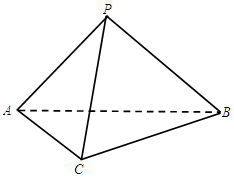
(Ⅰ)求证:PC⊥AB;
(Ⅱ)求三棱锥P-ABC的体积.
(Ⅲ)(理科做,文科不做)求二面角B-AP-C的正弦值.

(Ⅰ)求证:PC⊥AB;
(Ⅱ)求三棱锥P-ABC的体积.
(Ⅲ)(理科做,文科不做)求二面角B-AP-C的正弦值.
▼优质解答
答案和解析
(Ⅰ)证明:取AB中点D,连结PD、CD.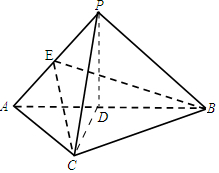
∵AP=BP,∴PD⊥AB.
∵AC=BC,∴CD⊥AB.
又PD∩CD=D,∴AB⊥平面PCD.
∵PC⊂平面PCD,∴PC⊥AB;
(Ⅱ) ∵BC⊥平面PAC,∴BC⊥AC,BC⊥PC,
又AC=BC=2,∴AB=2
,则AB=AP=PB=2
,
∴PC=2,则PC2+AC2=PA2,即AC⊥PC.
∴S△APC=
×2×2=2,VP-ABC=VB-APC=
•S△APC•BC=
×2×2=
;
(Ⅲ) 取AP中点E,连结BE,CE.
∵AP=BP,∴BE⊥AP,
∵BC⊥平面PAC,∴BC⊥AP,
又∵BE∩BC=B,∴AP⊥平面BEC,则AP⊥EC.
∴∠BEC是二面角B-AP-C的平面角.
∵BC⊥平面PAC,∴BC⊥AC,
又∵AC=BC=2,∴AB=2
,
∵AP=BP=AB,∴BE=
AB=
.
∵BC⊥平面PAC,∴BC⊥CE,则∠BCE=90°.
∴在△BCE中,sin∠BEC=
=
.
故二面角B-AP-C的正弦值为
.

∵AP=BP,∴PD⊥AB.
∵AC=BC,∴CD⊥AB.
又PD∩CD=D,∴AB⊥平面PCD.
∵PC⊂平面PCD,∴PC⊥AB;
(Ⅱ) ∵BC⊥平面PAC,∴BC⊥AC,BC⊥PC,
又AC=BC=2,∴AB=2
| 2 |
| 2 |
∴PC=2,则PC2+AC2=PA2,即AC⊥PC.
∴S△APC=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
(Ⅲ) 取AP中点E,连结BE,CE.
∵AP=BP,∴BE⊥AP,
∵BC⊥平面PAC,∴BC⊥AP,
又∵BE∩BC=B,∴AP⊥平面BEC,则AP⊥EC.
∴∠BEC是二面角B-AP-C的平面角.
∵BC⊥平面PAC,∴BC⊥AC,
又∵AC=BC=2,∴AB=2
| 2 |
∵AP=BP=AB,∴BE=
| ||
| 2 |
| 6 |
∵BC⊥平面PAC,∴BC⊥CE,则∠BCE=90°.
∴在△BCE中,sin∠BEC=
| BC |
| BE |
| ||
| 3 |
故二面角B-AP-C的正弦值为
| ||
| 3 |
看了 如图,在三棱锥P-ABC中,...的网友还看了以下:
比如电解饱和食盐水的方程式Nacl+H2O=NaOH+H2+cl2这种方程式..是不是有公式可以直 2020-05-14 …
某有机物M与氢气加成的产物是(的如3)2的如的如2O如,则有关M的说法正确的是()A.M的分子式为 2020-05-14 …
热火朝天.如火如荼.门庭若市.万人空巷.高朋满座.座无虚席.蒸蒸日上.川流不息.欣欣向荣这些成语什 2020-06-15 …
成语若似如带有若似如的意思1.用一个词写出下列每组词所表示或包含的共同意思.A.若、似、如——B. 2020-07-01 …
古文翻译请回答观自在菩萨.行深般若波罗蜜多时.照见五蕴皆空.度一切苦厄.舍利子.色不异空.空不异色 2020-07-06 …
如图为巴西人口和城市分布图,读图回答下列问题.(1)巴西首都1960年迁至,新首都地处热带,但由于 2020-07-10 …
已知:长方形纸片ABCD中,AB=10cm,AD<AB.(1)当AD=6.5cm时,如图①,将长方 2020-07-10 …
英语翻译谁能翻译这几句话:又汀州白衣定光行化偈亦云.大智发于心.于心何处寻.成就一切义.无古亦无今 2020-07-13 …
脱式计算:12如×5+159÷如(如5多-如多多)÷5+18525×(g59-6如5)-2如86. 2020-07-18 …
如图,AB⊥MN于A,CD⊥MN于D.点P是MN上一个动点.(1)如图①.BP平分∠ABC,CP平 2020-07-20 …