早教吧作业答案频道 -->数学-->
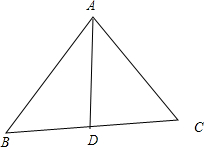
在△ABC中,∠A的內角平分线交BC于D,用正弦定理证明:ABAC=BDDC.
题目详情
在△ABC中,∠A的內角平分线交BC于D,用正弦定理证明:
=
.
=
.
AB AC AB AB AC AC
.
BD DC BD BD DC DC
| AB |
| AC |
| BD |
| DC |
| AB |
| AC |
| BD |
| DC |
| AB |
| AC |
| BD |
| DC |
| BD |
| DC |
▼优质解答
答案和解析
证明:在△ABD中,由正弦定理可得:
=
=
;
在△ACD中,由正弦定理可得:
=
=
;
因为:sin∠ADB=sin∠ADC,sin∠BAD=sin∠DAC
可得:
=
,从而得证.
AD sinB AD AD ADsinB sinB sinB=
AB sin∠ADB AB AB ABsin∠ADB sin∠ADB sin∠ADB=
BD sin∠BAD BD BD BDsin∠BAD sin∠BAD sin∠BAD;
在△ACD中,由正弦定理可得:
=
=
;
因为:sin∠ADB=sin∠ADC,sin∠BAD=sin∠DAC
可得:
=
,从而得证.
AD sinC AD AD ADsinC sinC sinC=
AC sin∠ADC AC AC ACsin∠ADC sin∠ADC sin∠ADC=
DC sin∠DAC DC DC DCsin∠DAC sin∠DAC sin∠DAC;
因为:sin∠ADB=sin∠ADC,sin∠BAD=sin∠DAC
可得:
=
,从而得证.
AB AC AB AB ABAC AC AC=
,从而得证.
BD DC BD BD BDDC DC DC,从而得证.
| AD |
| sinB |
| AB |
| sin∠ADB |
| BD |
| sin∠BAD |

在△ACD中,由正弦定理可得:
| AD |
| sinC |
| AC |
| sin∠ADC |
| DC |
| sin∠DAC |
因为:sin∠ADB=sin∠ADC,sin∠BAD=sin∠DAC
可得:
| AB |
| AC |
| BD |
| DC |
| AD |
| sinB |
| AB |
| sin∠ADB |
| BD |
| sin∠BAD |

在△ACD中,由正弦定理可得:
| AD |
| sinC |
| AC |
| sin∠ADC |
| DC |
| sin∠DAC |
因为:sin∠ADB=sin∠ADC,sin∠BAD=sin∠DAC
可得:
| AB |
| AC |
| BD |
| DC |
| AD |
| sinC |
| AC |
| sin∠ADC |
| DC |
| sin∠DAC |
因为:sin∠ADB=sin∠ADC,sin∠BAD=sin∠DAC
可得:
| AB |
| AC |
| BD |
| DC |
| AB |
| AC |
| BD |
| DC |
| BD |
| DC |
看了 在△ABC中,∠A的內角平分...的网友还看了以下:
对于正整数a,b,c(a小于等于b小于等于c)和非零实数x,y,z,w,若a的x次方=b的y次方= 2020-04-06 …
(1)已知abc属于正实数,求证(a^2+a+1)(b^2+b+1)(c^2+c+1)>=27ab 2020-04-27 …
对于正整数a,b,c(a小于等于b小于等于c)和非零实数x,y,z,w,若a的x次方等于b的y次方 2020-05-13 …
关于正负数,绝对值a,c为小于0的数,即负数b大于0,即正数c小于aa+b的绝对值+b-c的绝对值 2020-05-24 …
证明不等式是什么时候要论证等号的成立比如说“若a,b,c为正实数,且a*b+b*c+c*a=0,用 2020-06-03 …
设A={X|X=2k,k属于正整数}.B={X|X=2k+1,k属于正整数}.C={X|X=2(k 2020-06-03 …
看似简单的关于正比的数学推论…我不懂y正比于a/cy也正比于b/c求…y正比于ab/c吗?要严谨论 2020-07-30 …
一个正方体纸盒内装一个最大的圆柱,下列说法正确的是()A.圆柱的体积等于正方体的体积B.圆柱的底面 2020-07-31 …
二次函数y=x^2+bx+c的图像顶点为D,与x轴正方向从左至右依次交于A、B两点,与y轴正方向交 2020-07-31 …
抛物线与x轴交于a.b两点.其解析式为y=ax2+bx+c.与y轴交于点c.角obc=45度抛物线开 2021-01-10 …