早教吧作业答案频道 -->数学-->
△ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值.
题目详情
△ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值.
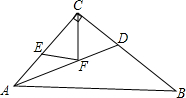 △ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值.
△ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值.


 △ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值.
△ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值.

▼优质解答
答案和解析
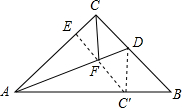 如图所示:将△ACD沿AD翻折得到△ADC′,连接DC′,过点C′作C′E⊥AC,
如图所示:将△ACD沿AD翻折得到△ADC′,连接DC′,过点C′作C′E⊥AC,
∵AD是∠CAB的角平分线,
∴△ACD与△ADC′关于AD对称.
∴点C′在AB上.
由翻折的性质可知:AC′=AC=4,.FC=FC′.
∴EF+FC=EF+FC′.
由垂线段最短可知:当C′E⊥AC时,C′E有最小值.
在Rt△ACB中,AB=
=4
,
∵C′E⊥AC,
∴△AEC′是等腰直角三角形,
∴EC′=
AC′=2
.
∴EF+CF的最小值是2
.
AC2+BC2 AC2+BC2 AC2+BC2 AC2+BC22+BC22=4
,
∵C′E⊥AC,
∴△AEC′是等腰直角三角形,
∴EC′=
AC′=2
.
∴EF+CF的最小值是2
.
2 2 2 2,
∵C′E⊥AC,
∴△AEC′是等腰直角三角形,
∴EC′=
AC′=2
.
∴EF+CF的最小值是2
.
2
2 2 2 22 2 2AC′=2
.
∴EF+CF的最小值是2
.
2 2 2 2.
∴EF+CF的最小值是2
.
2 2 2 2.
 如图所示:将△ACD沿AD翻折得到△ADC′,连接DC′,过点C′作C′E⊥AC,
如图所示:将△ACD沿AD翻折得到△ADC′,连接DC′,过点C′作C′E⊥AC,∵AD是∠CAB的角平分线,
∴△ACD与△ADC′关于AD对称.
∴点C′在AB上.
由翻折的性质可知:AC′=AC=4,.FC=FC′.
∴EF+FC=EF+FC′.
由垂线段最短可知:当C′E⊥AC时,C′E有最小值.
在Rt△ACB中,AB=
| AC2+BC2 |
| 2 |
∵C′E⊥AC,
∴△AEC′是等腰直角三角形,
∴EC′=
| ||
| 2 |
| 2 |
∴EF+CF的最小值是2
| 2 |
| AC2+BC2 |
| 2 |
∵C′E⊥AC,
∴△AEC′是等腰直角三角形,
∴EC′=
| ||
| 2 |
| 2 |
∴EF+CF的最小值是2
| 2 |
| 2 |
∵C′E⊥AC,
∴△AEC′是等腰直角三角形,
∴EC′=
| ||
| 2 |
| 2 |
∴EF+CF的最小值是2
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴EF+CF的最小值是2
| 2 |
| 2 |
∴EF+CF的最小值是2
| 2 |
| 2 |
看了 △ABC是等腰直角三角形,∠...的网友还看了以下:
采购员用一张1万元支票去购物.购单价为590元的A种物品若干件,又购单价为670元的B种物品若干件 2020-04-07 …
A、B两地相距6千米,甲、乙两人分别从A、B两地同时出发在两地间往返行走(到达另一地点后就马上返回 2020-04-26 …
已知平面直角坐标系中AB两点坐标分别为A(2,—3)B(4,—1)1.若C(a,o)D(a+3,o 2020-06-14 …
已知平面直角坐标系中AB两点坐标分别为A(2,—3)B(4,—1)1.若C(a,o)D(a+3,o 2020-06-14 …
如图7甲所示,用粘性材料粘在一起的A、B两物块静止于光滑水平面上,两物块的质量分别为mA=lkg、 2020-06-26 …
甲乙两辆车分别从A.B两地同时相对开出,乙车每小时行全程的20%,甲车比乙车早1/4小时到达A.B 2020-07-18 …
如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a、b满足a=3−b+ 2020-07-21 …
一个四位数,其千位数字、百位数字、十位数字、个位数字分别为A/B/C/D一个四位数,其千位数字、百 2020-07-29 …
如图所示,A球的质量为确定值m0,B球的质量m可以是任意值,忽略阻力以及其他部分的质量,则下列说法正 2020-11-10 …
A、B两车沿同一直线向同一方向运动,A车的速度VA=4m/s,B车的速度VB=10m/s.当B车运动 2020-11-30 …