早教吧作业答案频道 -->数学-->
如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.(1)求证:△AOE≌△COF;(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明
题目详情
如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.
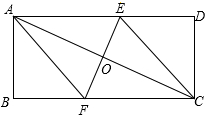
(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.

(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.


(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.

(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.

▼优质解答
答案和解析
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是AC的中点,
∴AO=CO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA);
(2) 四边形AFCE是菱形;理由如下:
理由是:由(1)△AOE≌△COF得:OE=OF
又∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC
∴平行四边形AFCE是菱形.
∠EAO=∠FCO AO=CO ∠AOE=∠COF ∠EAO=∠FCO ∠EAO=∠FCO ∠EAO=∠FCO AO=CO AO=CO AO=CO ∠AOE=∠COF ∠AOE=∠COF ∠AOE=∠COF
∴△AOE≌△COF(ASA);
(2) 四边形AFCE是菱形;理由如下:
理由是:由(1)△AOE≌△COF得:OE=OF
又∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC
∴平行四边形AFCE是菱形.
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是AC的中点,
∴AO=CO,
在△AOE和△COF中,
|
∴△AOE≌△COF(ASA);
(2) 四边形AFCE是菱形;理由如下:
理由是:由(1)△AOE≌△COF得:OE=OF
又∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC
∴平行四边形AFCE是菱形.
|
| ∠EAO=∠FCO | |
| AO=CO | |
| ∠AOE=∠COF |
| ∠EAO=∠FCO | |
| AO=CO | |
| ∠AOE=∠COF |
| ∠EAO=∠FCO | |
| AO=CO | |
| ∠AOE=∠COF |
| ∠EAO=∠FCO | |
| AO=CO | |
| ∠AOE=∠COF |
∴△AOE≌△COF(ASA);
(2) 四边形AFCE是菱形;理由如下:
理由是:由(1)△AOE≌△COF得:OE=OF
又∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC
∴平行四边形AFCE是菱形.
看了 如图,已知AC是矩形ABCD...的网友还看了以下:
某刑事案件的六个嫌疑分子A,B,C,D,E,F交待了以下材料:AB与F作案;BD与A作案;CB与E 2020-05-16 …
某刑事案件的六个嫌疑分子A,B,C,D,E,F交待了以下材料:某刑事案件的六个嫌疑分子A,B,C, 2020-05-16 …
设映射f:X->Y,A是X的子集,B也是X的子集,证明:(1)f(A并B)=f(A)并f(B)(2 2020-06-14 …
BE,CD交于A点,角DEA、角BCA的平分线相交于点F,你认为角F和角B、角D有什么等量关系 2020-06-15 …
角ABC的平分线BF与三角形ABC中角ACB的相邻外角的平分线CF相交于点F,过点F作DF\B角A 2020-06-27 …
某刑事案件的六个嫌疑分子A,B,C,D,E,F交待了以下材料:某刑事案件的六个嫌疑分子A,B,C, 2020-07-29 …
数学映射问题设映射f:X-Y,A属于X,B属于X,证明:(1)f(A并B)=f(A)并f(B)(2 2020-07-30 …
设f(x)在[a,b]上连续,在(a,b)内有二阶导数,连接点A(a,f(a)和B(b,f(b)) 2020-08-02 …
设f(x)在[a,b]上连续,在(a,b)内有二阶导数,连接点A(a,f(a)和B(b,f(b)) 2020-08-02 …
设f(x)在[a,b]连续,在(a,b)二阶可导,连接点A(a,f(a))和B(b,f(b))的直线 2020-12-28 …