已知：∠A是锐角且满足sinA=513，则sin（90°-A）=．

Question

已知：∠A是锐角且满足sinA= (5)/(13)，则sin（90°-A）=___．已知：∠A是锐角且满足sinA= (5)/(13)，则sin（90°-A）=___． (5)/(13)，则sin（90°-A）=___．(5)/(13) 5 13 5 5 13 13

Answer 1

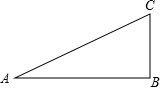如图，∵∠A是锐角且满足sinA=(5)/(13)，
∴设BC=5x，则AC=13x，
∵AC²=BC²+AB²，
∴AB=√(AC2-BC2)=√((13x)2-(5x)2)=12x，
∴sin（90°-A）=cosA=(AB)/(AC)=(12x)/(13x)=(12)/(13)．
故答案为：(12)/(13)． (5)/(13)513555131313，
∴设BC=5x，则AC=13x，
∵AC²2=BC²2+AB²2，
∴AB=√(AC2-BC2)=√((13x)2-(5x)2)=12x，
∴sin（90°-A）=cosA=(AB)/(AC)=(12x)/(13x)=(12)/(13)．
故答案为：(12)/(13)． √(AC2-BC2)

AC2-BC2

AC2-BC2

AC2-BC2AC2-BC22-BC22=√((13x)2-(5x)2)=12x，
∴sin（90°-A）=cosA=(AB)/(AC)=(12x)/(13x)=(12)/(13)．
故答案为：(12)/(13)． √((13x)2-(5x)2)

(13x)2-(5x)2

(13x)2-(5x)2

(13x)2-(5x)2(13x)2-(5x)22-(5x)22=12x，
∴sin（90°-A）=cosA=(AB)/(AC)=(12x)/(13x)=(12)/(13)．
故答案为：(12)/(13)． (AB)/(AC)ABACABABABACACAC=(12x)/(13x)=(12)/(13)．
故答案为：(12)/(13)． (12x)/(13x)12x13x12x12x12x13x13x13x=(12)/(13)．
故答案为：(12)/(13)． (12)/(13)1213121212131313．
故答案为：(12)/(13)． (12)/(13)1213121212131313．