如图所示，不可伸长的细绳长为L，一端固定在0点，另一端拴接一质量为m的小球．将小球拉至与0等高，细绳处于伸直状态的位置后由静止释放，在小球由静止释放到运动至最低点的过程中，

Question

如图所示，不可伸长的细绳长为L，一端固定在0点，另一端拴接一质量为m的小球．将小球拉至与0等高，细绳处于伸直状态的位置后由静止释放，在小球由静止释放到运动至最低点的过程中，小球所受阻力做的功为W，重力加速度为g，则小球到达最低点时（　　）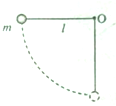

A. 向心加速度度a=

(2(mgl+w))/(ml)

B. 向心加速度a=

(2(mgl-w))/(ml)

C. 绳的拉力F=

(3mgl+2w)/(l)

D. 绳的拉力F=

(2(mgl+w))/(l)

如图所示，不可伸长的细绳长为L，一端固定在0点，另一端拴接一质量为m的小球．将小球拉至与0等高，细绳处于伸直状态的位置后由静止释放，在小球由静止释放到运动至最低点的过程中，小球所受阻力做的功为W，重力加速度为g，则小球到达最低点时（　　）

如图所示，不可伸长的细绳长为L，一端固定在0点，另一端拴接一质量为m的小球．将小球拉至与0等高，细绳处于伸直状态的位置后由静止释放，在小球由静止释放到运动至最低点的过程中，小球所受阻力做的功为W，重力加速度为g，则小球到达最低点时（　　）

A. 向心加速度度a=

(2(mgl+w))/(ml)

a=(2(mgl+w))/(ml)(2(mgl+w))/(ml)2(mgl+w)ml2(mgl+w)2(mgl+w)mlml

B. 向心加速度a=

(2(mgl-w))/(ml)

a=(2(mgl-w))/(ml)(2(mgl-w))/(ml)2(mgl-w)ml2(mgl-w)2(mgl-w)mlml

C. 绳的拉力F=

(3mgl+2w)/(l)

F=(3mgl+2w)/(l)(3mgl+2w)/(l)3mgl+2wl3mgl+2w3mgl+2wll

D. 绳的拉力F=

(2(mgl+w))/(l)

F=(2(mgl+w))/(l)(2(mgl+w))/(l)2(mgl+w)l2(mgl+w)2(mgl+w)ll

Answer 1

A、根据动能定理得：mgL+W=(1)/(2)mv2，则向心加速度为：a=(v2)/(L)=(2(mgL+W))/(mL)，故A正确，B错误．
C、在最低点，根据牛顿第二定律得：F-mg=m(v2)/(L)，解得绳子的拉力为：F=mg+m(v2)/(L)=(3mgL+2W)/(L)，故C正确，D错误．
故选：AC． mgL+W=(1)/(2)12111222mv2，则向心加速度为：a=(v2)/(L)=(2(mgL+W))/(mL)，故A正确，B错误．
C、在最低点，根据牛顿第二定律得：F-mg=m(v2)/(L)，解得绳子的拉力为：F=mg+m(v2)/(L)=(3mgL+2W)/(L)，故C正确，D错误．
故选：AC． 2，则向心加速度为：a=(v2)/(L)=(2(mgL+W))/(mL)，故A正确，B错误．
C、在最低点，根据牛顿第二定律得：F-mg=m(v2)/(L)，解得绳子的拉力为：F=mg+m(v2)/(L)=(3mgL+2W)/(L)，故C正确，D错误．
故选：AC． (v2)/(L)v2Lv2v2v22LLL=(2(mgL+W))/(mL)2(mgL+W)mL2(mgL+W)2(mgL+W)2(mgL+W)mLmLmL，故A正确，B错误．
C、在最低点，根据牛顿第二定律得：F-mg=m(v2)/(L)，解得绳子的拉力为：F=mg+m(v2)/(L)=(3mgL+2W)/(L)，故C正确，D错误．
故选：AC． F-mg=m(v2)/(L)v2Lv2v2v22LLL，解得绳子的拉力为：F=mg+m(v2)/(L)=(3mgL+2W)/(L)，故C正确，D错误．
故选：AC． mg+m(v2)/(L)v2Lv2v2v22LLL=(3mgL+2W)/(L)，故C正确，D错误．
故选：AC． (3mgL+2W)/(L)3mgL+2WL3mgL+2W3mgL+2W3mgL+2WLLL，故C正确，D错误．
故选：AC．