早教吧作业答案频道 -->数学-->
如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF(1)求证:AF=CF;(2)若∠BAF=35°,求∠BFC的度数.
题目详情
如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF
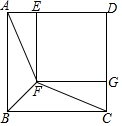
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.
▼优质解答
答案和解析
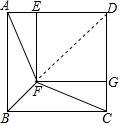 (1)证明:∵四边形ABCD和四边形DEFG都是正方形,
(1)证明:∵四边形ABCD和四边形DEFG都是正方形,
∴AD=CD,ED=GD,FE=FG.
∴AD-ED=CD-GD.
∴AE=CG.
在△AFE和△CFG中
,
∴△AFE≌△CFG(SAS),
∴AF=CF;
(2) 由(1)得△AEF≌△CGF,
∴∠AFE=∠CFG.
又∵AB∥EF,∠BAF=35°,
∴∠AFE=∠CFG=∠BAF=35°.
连接DF,
∵四边形DEFG是正方形,
∴∠DFG=45°.
∴∠BFC=180°-∠CFG-∠GFD=180°-35°-45°=100°.
即∠BFC=100°.
 (1)证明:∵四边形ABCD和四边形DEFG都是正方形,
(1)证明:∵四边形ABCD和四边形DEFG都是正方形,∴AD=CD,ED=GD,FE=FG.
∴AD-ED=CD-GD.
∴AE=CG.
在△AFE和△CFG中
|
∴△AFE≌△CFG(SAS),
∴AF=CF;
(2) 由(1)得△AEF≌△CGF,
∴∠AFE=∠CFG.
又∵AB∥EF,∠BAF=35°,
∴∠AFE=∠CFG=∠BAF=35°.
连接DF,
∵四边形DEFG是正方形,
∴∠DFG=45°.
∴∠BFC=180°-∠CFG-∠GFD=180°-35°-45°=100°.
即∠BFC=100°.
看了 如图,四边形ABCD和四边形...的网友还看了以下:
读我国某地区等高线图(A地形区发育一河流),回答3~4题。3.对A处河流方面的叙述正确的是()A. 2020-05-01 …
如图,在四边形abCd中,已知∠A=∠C,AD∥BC,求证四边形abcd是平行四边形那个图就是平常 2020-05-13 …
现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,∠A=∠D=30°.① 2020-05-16 …
要表示各个部分量和总量之间的关系,应绘制()统计图A扇形B折线C条形D前面三种都可以 2020-05-20 …
五(2)班要绘制一个反映参加课外小组的人数占全班总人数情况的统计图.应选用()统计图.A.条形B. 2020-06-05 …
1/将人的身高增长情况制成折线统计图,一般会发现()趋势.A直线上升B成正比例增长C先上升后下降D 2020-07-31 …
要表示每月用水量与全年用水量之间的关系,最好选用()统计图.A.条形B.折线C.扇形D.以上三种都 2020-07-31 …
现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,∠A=∠D=30°.将 2020-08-02 …
在excel中,最适合反映数据之间量的变化快慢的一种图表类型是什么图?A.柱形图B.散点图C.饼图D 2020-11-01 …
a四方+b四方+c四方+d四方=4abcd,abcd为正数,用abcd围成的图形是什么图形不是正方形 2020-11-07 …