早教吧作业答案频道 -->物理-->
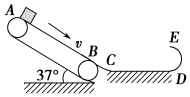
如图所示的装置由传送带AB、水平地面CD、光滑半圆形轨道DE三部分组成.一质量为5kg的物块从静止开始沿倾角为37°的传送带上滑下.若传送带顺时针运动,其速度v=10m/s,传送带与水平地面
题目详情
如图所示的装置由传送带AB、水平地面CD、光滑半圆形轨道DE三部分组成.一质量为5kg的物块从静止开始沿倾角为37°的传送带上滑下.若传送带顺时针运动,其速度v=10m/s,传送带与水平地面之间通过光滑圆弧BC相连,圆弧BC长度可忽略不计,传送带AB长度为LAB=16m,水平地面长度为LCD=6.3m,半圆轨道DE的半径R=1.125m,物块与水平地面间、传送带间的动摩擦因数均为μ=0.5.求:(sin 37°=0.6,cos 37°=0.8)
(1)物块在传送带上运动的时间t;
(2)物块到达D点时对D点的压力大小;
(3)物块从E点抛出后的落地点与D点的距离.

(1)物块在传送带上运动的时间t;
(2)物块到达D点时对D点的压力大小;
(3)物块从E点抛出后的落地点与D点的距离.
▼优质解答
答案和解析
(1)刚开始运动时,对物块受力分析,由牛顿第二定律可知:
mgsin37°+μmgcos37°=ma1
代入数据解得:a1=10 m/s2
物块与传送带达到共同速度时有:v=a1t1,
代入数据解得:t1=1 s
物块的位移为:x=
a1t12=
×10×12m=5 m
此后对物块受力分析可知:
mgsin 37°-μmgcos 37°=ma2
代入数据解得:a2=2 m/s
物块在传送带上的第二段运动过程有:
LAB-x=vt2+
a2t22
代入数据解得:t2=1 s
故物块在传送带上运动的总时间为:t=t1+t2=2 s
(2)物块到达传送带底端的末速度为:v2=v+a2t2=10+2×1=12 m/s
在水平地面CD上,物块做匀减速直线运动,其加速度大小为:a=
=μg=5 m/s2
设物块到达D点时的速度为v3,则有:
vD2-v22=-2aLCD
代入数据解得:v3=9 m/s
设此时D点对物块的支持力为FN,根据牛顿第二定律,有:
FN-mg=m
代入数据解得:FN=410 N
根据牛顿第三定律可知,物块对D点的压力大小为410 N.
(3)物块沿半圆轨道从D点运动到E点的过程机械能守恒,设物块经过E点时的速度为vE,根据机械能守恒定律有:
mvD2=
mvE2+2mgR
代入数据解得:vE=6 m/s
物块从E点抛出后做平抛运动,有:
s=vEt3,
2R=
gt32.
联立并代入数据解得:s=
m.
答:(1)物块在传送带上运动的时间是2 s;
(2)物块到达D点时对D点的压力大小是410 N;
(3)物块从E点抛出后的落地点与D点的距离是
m.
mgsin37°+μmgcos37°=ma1
代入数据解得:a1=10 m/s2
物块与传送带达到共同速度时有:v=a1t1,
代入数据解得:t1=1 s
物块的位移为:x=
| 1 |
| 2 |
| 1 |
| 2 |
此后对物块受力分析可知:
mgsin 37°-μmgcos 37°=ma2
代入数据解得:a2=2 m/s
物块在传送带上的第二段运动过程有:
LAB-x=vt2+
| 1 |
| 2 |
代入数据解得:t2=1 s
故物块在传送带上运动的总时间为:t=t1+t2=2 s
(2)物块到达传送带底端的末速度为:v2=v+a2t2=10+2×1=12 m/s
在水平地面CD上,物块做匀减速直线运动,其加速度大小为:a=
| μmg |
| m |
设物块到达D点时的速度为v3,则有:
vD2-v22=-2aLCD
代入数据解得:v3=9 m/s
设此时D点对物块的支持力为FN,根据牛顿第二定律,有:
FN-mg=m
| ||
| R |
代入数据解得:FN=410 N
根据牛顿第三定律可知,物块对D点的压力大小为410 N.
(3)物块沿半圆轨道从D点运动到E点的过程机械能守恒,设物块经过E点时的速度为vE,根据机械能守恒定律有:
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:vE=6 m/s
物块从E点抛出后做平抛运动,有:
s=vEt3,
2R=
| 1 |
| 2 |
联立并代入数据解得:s=
9
| ||
| 5 |
答:(1)物块在传送带上运动的时间是2 s;
(2)物块到达D点时对D点的压力大小是410 N;
(3)物块从E点抛出后的落地点与D点的距离是
9
| ||
| 5 |
看了 如图所示的装置由传送带AB、...的网友还看了以下:
物理的滑轮还有浮力,明天中考了.如图的横向拉东西怎么算还有:F浮=G排=ρ液·g·V排所以P物gV排 2020-03-30 …
高三物理的v²=gR①1/2mV²=mg2R+1/2mv²②这两条式子怎么合并得出大V=?怎么高三物 2020-03-31 …
有道题说一物体在X轴方向速度为-Rwsin(wt),Y轴方向速度为Rwcos(wt),(R、w为常 2020-05-13 …
九6.上g的Cl溶解在vL水中,所得溶液的密度为ρg•mL-v,质量分数为w,物质的量浓度为cmo 2020-05-14 …
物体的体积为v物,把物体放入液体中排开液体的体积为v排.则下列说法正确的是A.物体在液体中收到浮力 2020-05-22 …
一个梯形物体浸没在水中,如图所示,水的密度为ρ,深度为H,物块高度为h,体积为V,较小的下底面面积 2020-06-03 …
一道很简单的化学平衡题物质A与B化合成C(A,B,C均为气体)的反应中,在不同的温度下,经t秒后, 2020-06-17 …
(2012•金山区一模)如图甲所示,某同学在水平面上用水平力拉一质量为1kg的物块,使物块由静止开 2020-06-25 …
物体做简谐运动,通过A点时的速度为v,经1s后物体第一次以速度v通过B点,再经过1s物体紧接着又通 2020-06-29 …
可逆反应平衡时,各物质反应速率不为零,但v=△c/△t,△c=0,所以v=0,这不是矛盾了吗?按理 2020-06-29 …