早教吧作业答案频道 -->数学-->
已知BC是O的直径,BF是弦,AD过圆心O,AD⊥BF,AE⊥BC于E,连接FC.(1)如图1,若OE=2,求CF;(2)如图2,连接DE,并延长交FC的延长线于G,连接AG,请你判断直线AG与O的位置关系,并说明理
题目详情
已知BC是 O的直径,BF是弦,AD过圆心O,AD⊥BF,AE⊥BC于E,连接FC.
(1)如图1,若OE=2,求CF;
(2)如图2,连接DE,并延长交FC的延长线于G,连接AG,请你判断直线AG与 O的位置关系,并说明理由.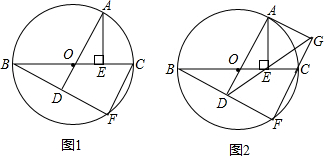
(1)如图1,若OE=2,求CF;
(2)如图2,连接DE,并延长交FC的延长线于G,连接AG,请你判断直线AG与 O的位置关系,并说明理由.

▼优质解答
答案和解析
(1)∵BC是 O的直径,AD过圆心O,AD⊥BF,AE⊥BC于E,
∴∠AEO=∠BDO=90°,OA=OB,
在△AEO和△BDO中,
,
∴△AEO≌△BDO(AAS),
∴OE=OD=2,
∵BC是 O的直径,
∴∠CFB=90°,即CF⊥BF,
∴OD∥CF,
∵O为BC的中点,
∴OD为△BFC的中位线,
∴CF=2OD=4;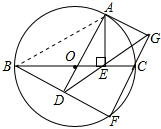
(2)直线AG与 O相切,理由如下:
连接AB,如图所示:
∵OA=OB,OE=OD,
∴△OAB与△ODE为等腰三角形,
∵∠AOB=∠DOE,
∴∠ADG=∠OED=∠BAD=∠ABO,
∵∠GDF+∠ADG=90°=∠BAD+∠ABD,
∴∠GDF=∠ABD,
∵OD为△BFC的中位线,
∴BD=DF,
在△ABD和△GDF中,
,
∴△ABD≌△GDF(ASA),
∴AD=GF,
∵AD⊥BF,GF⊥BF,
∴AD∥GF,
∴四边形ADFG为矩形,
∴AG⊥OA,
∴直线AG与 O相切.
∴∠AEO=∠BDO=90°,OA=OB,
在△AEO和△BDO中,
|
∴△AEO≌△BDO(AAS),
∴OE=OD=2,
∵BC是 O的直径,
∴∠CFB=90°,即CF⊥BF,
∴OD∥CF,
∵O为BC的中点,
∴OD为△BFC的中位线,
∴CF=2OD=4;

(2)直线AG与 O相切,理由如下:
连接AB,如图所示:
∵OA=OB,OE=OD,
∴△OAB与△ODE为等腰三角形,
∵∠AOB=∠DOE,
∴∠ADG=∠OED=∠BAD=∠ABO,
∵∠GDF+∠ADG=90°=∠BAD+∠ABD,
∴∠GDF=∠ABD,
∵OD为△BFC的中位线,
∴BD=DF,
在△ABD和△GDF中,
|
∴△ABD≌△GDF(ASA),
∴AD=GF,
∵AD⊥BF,GF⊥BF,
∴AD∥GF,
∴四边形ADFG为矩形,
∴AG⊥OA,
∴直线AG与 O相切.
看了 已知BC是O的直径,BF是弦...的网友还看了以下:
一个正方体的每个面分别写有“奋,斗,成,就,未,来”.根据图中正方体A、B、C三种状态所显示的字, 2020-04-06 …
读下图,据此回答1-3题:1.四幅图中位在亚洲与北美洲边界的图是:A.a图B.b图C.c图D.d图 2020-05-02 …
下列四幅图是我们在实验室或课堂上做过的一些实验.则:A图小纸片能跳起来的原因是.B图探究的问题是. 2020-05-02 …
写出下列四张气候坐标图的气候类型A图的气候类型是B图的气候类型是C图的气候类型是D图的气候类型是 2020-05-02 …
下图是几种鸟足图,分析比较说明它们适于何种生活习性。A图适于。B图适于。C图适于。D图适于。E图适 2020-05-02 …
如图,在三角形ABC中,∠ACB=90°,AC=BC,直线l经过点C,AD⊥l于点D,BE垂直l于 2020-05-15 …
电工基础(电路基础)复杂电阻电路的等效转换a图怎么转换成b图和c图的,求前辈们详细说明下 2020-05-17 …
(2014•雨花台区一模)如图是课本上的一些演示实验或插图,请你根据要求填空:(1)A图中的实验得 2020-06-19 …
(2013•滨湖区二模)如图,已知二次函数y=ax2+bx+c的图象交x轴的负半轴于点A(-5,0 2020-07-20 …
关于二次函数y=ax2+bx+c图象有下列命题:(1)当c=0时,函数的图象经过原点;(2)当c> 2020-08-01 …