早教吧作业答案频道 -->数学-->
如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.(1)求证:FG=BE;(2)探索点F是否
题目详情
如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.
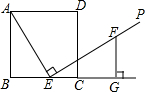
(1)求证:FG=BE;
(2)探索点F是否在∠DCG的平分线上,并说明你的理由.

(1)求证:FG=BE;
(2)探索点F是否在∠DCG的平分线上,并说明你的理由.
▼优质解答
答案和解析
(1)证明:∵EP⊥AE,
∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°,
∴∠GEF=∠BAE,
又∵FG⊥BC,
∴∠ABE=∠EGF=90°,
在△ABE与△EGF中,
,
∴△ABE≌△EGF(AAS),
∴FG=BE;
(2) 点F在∠DCG的平分线上,理由如下:
连接CF,如图:
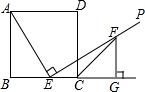
由(1)知:BC=AB=EG,
∴BC-EC=EG-EC,
∴BE=CG,
又∵FG=BE,
∴FG=CG,
又∵∠CGF=90°,
∴∠FCG=45°=
∠DCG,
∴CF平分∠DCG.
∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°,
∴∠GEF=∠BAE,
又∵FG⊥BC,
∴∠ABE=∠EGF=90°,
在△ABE与△EGF中,
|
∴△ABE≌△EGF(AAS),
∴FG=BE;
(2) 点F在∠DCG的平分线上,理由如下:
连接CF,如图:

由(1)知:BC=AB=EG,
∴BC-EC=EG-EC,
∴BE=CG,
又∵FG=BE,
∴FG=CG,
又∵∠CGF=90°,
∴∠FCG=45°=
| 1 |
| 2 |
∴CF平分∠DCG.
看了如图,E是正方形ABCD的边B...的网友还看了以下:
小珍想出了一个测量池塘对岸的AB两点距离的办法,如图:先分别从池塘的两端A、B引两条直线AC、BC 2020-04-07 …
不同物种的DNA分子的特异性主要取决于①(A+G)/(T+C)的不同 ②(A+T)/(G+C)的不 2020-05-17 …
6.有一核酸分子,其碱基比是A+G/T+C=1.5,试推断该核酸是?A.信使RNA B.转运RNA 2020-05-17 …
(2014•崇明县一模)已知2A(g)+B(g)→2C(g)+Q.下列说法或表达正确的是()A.使 2020-05-17 …
小珍想出了一个测量池塘对岸的AB两点距离的办法,如图:先分别从池塘的两端A、B引两条直线AC、BC 2020-07-11 …
若函数f(x),g(x)的定义域都是R,则f(x)>g(x)(x∈R)的充要条件是?A.存在一个属 2020-08-02 …
一道八年级生物填空题下面的益处与害处是谁的功与过?A酿酒或食用B,提取药物C,制作副食品D,使人、动 2020-11-01 …
对达到平衡状态的下列各可逆反应,加压和降温都能使平衡逆向移动的是()A.2NO2(g)═2NO(g) 2020-12-15 …
设f(x),g(x)在[a,b]上连续,在(a,b)内可导,且f'(x)=g'(x),x属于(a,b 2020-12-23 …
求证一道数学题,关于三角形的在三角形ABC中,作点B到AC边上的高BE,点C到AB边上的高CF.在B 2021-02-05 …