早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.(1)求∠NMB的度数;(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;(3)你发
题目详情
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
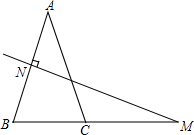
(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;
(3)你发现有什么样的规律性,试证明之.

(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;
(3)你发现有什么样的规律性,试证明之.
▼优质解答
答案和解析
(1)∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠ACB=70°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=20°;
(2)∵在△ABC中,AB=AC,∠A=70°,
∴∠ABC=∠ACB=55°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=35°;
(3)∠NMB=
∠A.
理由:∵在△ABC中,AB=AC,
∴∠ABC=∠ACB=
,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=
∠A.
∴∠ABC=∠ACB=70°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=20°;
(2)∵在△ABC中,AB=AC,∠A=70°,
∴∠ABC=∠ACB=55°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=35°;
(3)∠NMB=
| 1 |
| 2 |
理由:∵在△ABC中,AB=AC,
∴∠ABC=∠ACB=
| 180°-∠A |
| 2 |
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴MN⊥AB,
∴∠NMB=90°-∠ABC=
| 1 |
| 2 |
看了如图,在△ABC中,AB=AC...的网友还看了以下:
如图所示,长方形ABCD与长方形BEFG等长等宽,如将长方形BEFG向右平移,距离为EF.长方形AB 2020-03-31 …
如图,有一个长3分米,宽和高都是1分米的礼品箱,如果用绳子将礼品箱如图捆扎,打结处共用2分米.一要 2020-04-27 …
如图1,在边 长为a的大正方形中剪去一个边长为b的小正方形再将图中的阴影部分剪拼成一个长方形如图2 2020-05-16 …
如图1,边长为a的大正方形中有一个边长为b的小正方形,若将图1中的阴影部分拼成一个长方形如图2,比 2020-05-17 …
如图一个底面长30分米,宽10分米,高12分米的长方体水池,存有四分之三池水,请问:(1)将一个高 2020-06-17 …
如图一个底面长30分米,宽10分米,高12分米的长方体水池,存有四分之三池水,请问:(1)将一个高 2020-06-17 …
如图,有一个长5分米、宽和高都是3分米的长方体硬纸箱,如果用绳子将箱子横着捆两道,长着捆一道,打结 2020-07-12 …
如图①,边长为a的大正方形中有一个边长为b的小正方形.如图所示,边长为a的大正方形中有一个边长为b 2020-07-13 …
如图1在推导图的面积公式时,将圆品均分成18份,拼成一个近似的长方形如图①在推导圆的面积公式时,将圆 2020-11-28 …
一个长方体鱼缸,长8分米,宽4分米,高位5分米.将一个假山石全部浸如缸内,水面上升了5厘米.这个假山 2021-01-01 …