早教吧作业答案频道 -->数学-->
如图所示,酒杯的杯体轴截面是抛物线x2=2py(p>0)的一部分,若将半径为r(r>0)的玻璃球放入杯中,可以触及酒杯底部(即抛物线的顶点),则r的最大值为()A.12B.1C.2D.4
题目详情
如图所示,酒杯的杯体轴截面是抛物线x2=2py (p>0)的一部分,若将半径为r(r>0)的玻璃球放入杯中,可以触及酒杯底部(即抛物线的顶点),则r的最大值为( )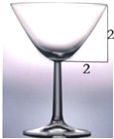
A. 1 2
B. 1
C. 2
D. 4
▼优质解答
答案和解析
设小球圆心(0,r),抛物线上点(x,y)
则点(x,y)到圆心距离平方为:r2=x2+(y-r)2=2py+(y-r)2=y2+2(p-r)y+r2
若r2最小值在(0,0)时取到,则小球触及杯底
故此二次函数的对称轴位置应在y轴的左侧,所以p-r≥0,所以r≤p,
所以0所以r的最大值为p,
又由题意,抛物线方程为x2=2y,p=1,
故选:B.
则点(x,y)到圆心距离平方为:r2=x2+(y-r)2=2py+(y-r)2=y2+2(p-r)y+r2
若r2最小值在(0,0)时取到,则小球触及杯底
故此二次函数的对称轴位置应在y轴的左侧,所以p-r≥0,所以r≤p,
所以0
又由题意,抛物线方程为x2=2y,p=1,
故选:B.
看了如图所示,酒杯的杯体轴截面是抛...的网友还看了以下:
左边一个提手,右边一个及是什么字?谢谢哦 2020-04-09 …
关于函数y=4sinx,x∈-π,π的单调性叙述,下列错在哪里?请指出并加以改正1.在-π,0上是 2020-04-27 …
0.53是由5个0.1和3个0.01组成的?请纠正?为什么这样做?请说出基本原理及其公式好吗?是不 2020-04-27 …
已知圆M:(x+3a)2+y2=16a2(a>0)及定点N(3a,0),点P是圆M上的动点,点G在 2020-05-15 …
左边一个足字旁,右边一个及是什么字最好注明出处和字义,谢谢了. 2020-05-17 …
请问函数的驻点和极值点的区别以及导数为0的关系1是不是驻点导数肯定为0?2是不是导数为0一定是驻点 2020-05-20 …
一元二次方程恒成立条件ax²+bx+c≥0及ax²+bx+c≤0的恒成立条件?请重点讨论a<0,a 2020-05-24 …
一个人和一个及是什么字 2020-06-11 …
单人旁,一个及是什么字? 2020-06-11 …
设在[0,1]上,f〃(x)>0,则f′(0),f′(1),f(1)-f(0)或f(0)-f(1) 2020-06-18 …