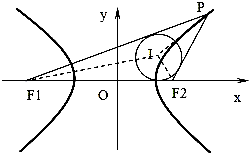
已知点P为双曲线=1（a＞0，b＞0）右支上一点，F1，F2分别为双曲线的左右焦点，且|F1F2|=，I为三角形PF1F2的内心，若S=S+λS△成立，则λ的值为（）A．B．C．D．

Question

已知点P为双曲线=1（a＞0，b＞0）右支上一点，F₁，F₂分别为双曲线的左右焦点，且|F₁F₂|=，I为三角形PF₁F₂的内心，若S=S+λS_△成立，则λ的值为（　　）

A．  B． C．    D．

Answer 1

D【考点】双曲线的简单性质．

【专题】圆锥曲线的定义、性质与方程．

【分析】设△PF₁F₂的内切圆半径为r，由|PF₁|﹣|PF₂|=2a，|F₁F₂|=2c，用△PF₁F₂的边长和r表示出等式中的

三角形的面积，解此等式求出λ．

【解答】设△PF₁F₂的内切圆半径为r，

由双曲线的定义得|PF₁|﹣|PF₂|=2a，|F₁F₂|=2c，

S_△IPF1 =|PF₁|•r，S_△IPF2=|PF₂|•r，S_△IF1F2=•2c•r=cr，

由题意得：|PF₁|•r=|PF₂|•r+λcr，

故λ==，

∵|F₁F₂|=，

∴=

∴

∴=

故选D．

【点评】本题考查双曲线的定义和简单性质，考查三角形面积的计算，考查利用待定系数法求出参数的值．