早教吧作业答案频道 -->数学-->
定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若垂线与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做“和谐点”.如图1,矩形ABOC的周长的数值与面积的数值
题目详情
定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若垂线与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做“和谐点”.
如图1,矩形ABOC的周长的数值与面积的数值相等,则点A是“和谐点”
(1)判断点E(2,3),F(4,4)是否为“和谐点”;
(2)如图2,若点P(a,b)是双曲线y=
上的“和谐点”,求满足条件的所有P点坐标.
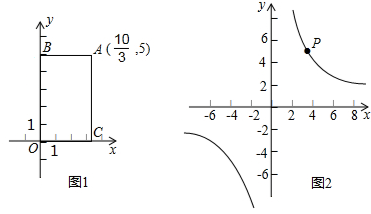
如图1,矩形ABOC的周长的数值与面积的数值相等,则点A是“和谐点”
(1)判断点E(2,3),F(4,4)是否为“和谐点”;
(2)如图2,若点P(a,b)是双曲线y=
| 18 |
| x |
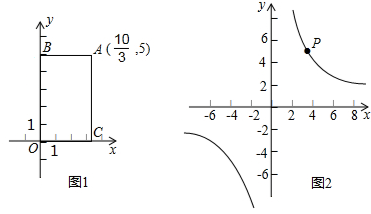
▼优质解答
答案和解析
(1)根据在平面直角坐标系中,过一点分别作坐标轴的垂线,若垂线与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做“和谐点”,
∵点E(2,3),2×(2+3)=10,2×3=6,
∴10≠6,
∴E点不是“和谐点”,
∵点F(4,4),2×(4+4)=16,4×4=16,
∴16=16,
∴F点是“和谐点”;
(2)设P点坐标为:(x,
),由题意得出:18=2|x+
|,
当18=2(x+
)
整理得出:x2-9x+18=0,
解得:x1=3,x2=6,
当-18=2(x+
)
整理得出:x2+9x+18=0,
解得:x3=-3,x4=-6,
∴P点坐标为:(3,6),(6,3),(-3,-6),(-6,-3).
∵点E(2,3),2×(2+3)=10,2×3=6,
∴10≠6,
∴E点不是“和谐点”,
∵点F(4,4),2×(4+4)=16,4×4=16,
∴16=16,
∴F点是“和谐点”;
(2)设P点坐标为:(x,
| 18 |
| x |
| 18 |
| x |
当18=2(x+
| 18 |
| x |
整理得出:x2-9x+18=0,
解得:x1=3,x2=6,
当-18=2(x+
| 18 |
| x |
整理得出:x2+9x+18=0,
解得:x3=-3,x4=-6,
∴P点坐标为:(3,6),(6,3),(-3,-6),(-6,-3).
看了 定义:在平面直角坐标系中,过...的网友还看了以下:
我的定义:两组对边分别平行的四边形是平行四边形.请在同一平面坐标系中,画图并探索.①画出函数y=2 2020-05-12 …
求坐标上两点距离定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且点位长度相同) 2020-06-05 …
对于两条平行直线和圆的位置关系定义如下:若两直线中至少有一条与圆相切,则称该位置关系为“平行相切” 2020-07-26 …
我国已经建立了社会主义公平保障体系,它包括[]①权利公平和机会公平②义务公平和分配公平③规则公平和 2020-07-29 …
将平面直角坐标系中的纵轴o顺时针旋转30度构成一个斜坐标系xoy,平面任意一点p关于斜坐标系的坐标 2020-07-30 …
新型的社会主义民族关系是()A.援助与被援助的关系B.平等、尊重、友爱、互助C.统治与被统治的关系D 2020-11-02 …
在土耳其建国和改革的过程中,逐渐形成了一套完整的政治思想理论体系,被称为“凯末尔主义”。包括六大原则 2020-11-27 …
我国的民族关系是完全新型的社会主义民族关系,是()A.平等、团结、互助、和谐的关系B.平等、团结、包 2020-12-01 …
两岸达成“九二共识”以来,两岸关系整体上平稳发展。两岸关系和平发展的政治基础是()A.一国两制B.坚 2020-12-20 …
根据要求,回答下列问题:(1)中国特色社会主义理论体系包括(2)我国在社会主义初级阶段的主要矛盾:( 2021-01-01 …