如图，由同一点O出发的两公交车分别沿道路L1、L2行驶且两公路分别经过A、B两个小区门口．（1）现准备在∠AOB内建一个加油站，要求加油站的位置点P到两个小区门口A、B的距离相

Question

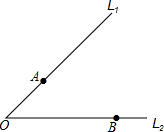如图，由同一点O出发的两公交车分别沿道路L ₁ 、L ₂ 行驶且两公路分别经过A、B两个小区门口．
（1）现准备在∠AOB内建一个加油站，要求加油站的位置点P到两个小区门口A、B的距离相等，且P到L ₁ 、L ₂ 的距离也相等，请用尺规作出点P（不需要写做法，保留作图痕迹）
（2）在（1）的条件下，过点P作PM⊥OA于M，作PN⊥OB于点N（不需要用圆规，用三角尺作出即可）则线段AM与BN有什么数量关系？请说明理由．

Answer 1

考点：
作图—应用与设计作图
专题：

分析：
（1）利用角平分线的性质与判定以及线段垂直平分线的性质与作法得出即可；（2）结合角平分线的性质以及线段垂直平分线的性质以及HL定理得出即可．

（1）连接A、B两点，作出线段AB的垂直平分线，再作出∠AOB的平分线，两线的交点即为点P．（2）AM=BN，理由：连接PA、PB．∵OP平分∠AOB，PM⊥OA，PN⊥OB，∴PM=PN，∵P在线段AB的垂直平分线上，∴PA=PB，在Rt△PMA和Rt△PNB中，∵PM=PNPA=PB，∴Rt△PMA≌Rt△PNB（HL），∴AM=BN．
点评：
此题主要考查了应用设计与作图以及全等三角形的判定与性质，熟练应用角平分线的性质以及线段垂直平分线的性质是解题关键．