早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=12,OB=4,OE=2.(1)求直线AB和反比例函数的解析式;(2)求△OC
题目详情
如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=
,OB=4,OE=2.
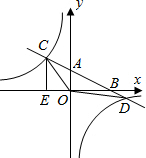
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
| 1 |
| 2 |

(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
▼优质解答
答案和解析
(1)∵OB=4,OE=2,
∴BE=2+4=6.
∵CE⊥x轴于点E,tan∠ABO=
=
=
.
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(-2,3).
设直线AB的解析式为y=kx+b,则
,
解得
.
故直线AB的解析式为y=-
x+2.
设反比例函数的解析式为y=
(m≠0),
将点C的坐标代入,得3=
,
∴m=-6.
∴该反比例函数的解析式为y=-
.
(2)联立反比例函数的解析式和直线AB的解析式可得
,
可得交点D的坐标为(6,-1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8.
∴BE=2+4=6.
∵CE⊥x轴于点E,tan∠ABO=
| AO |
| BO |
| CE |
| BE |
| 1 |
| 2 |
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(-2,3).
设直线AB的解析式为y=kx+b,则
|
解得
|
故直线AB的解析式为y=-
| 1 |
| 2 |
设反比例函数的解析式为y=
| m |
| x |
将点C的坐标代入,得3=
| m |
| -2 |
∴m=-6.
∴该反比例函数的解析式为y=-
| 6 |
| x |
(2)联立反比例函数的解析式和直线AB的解析式可得
|
可得交点D的坐标为(6,-1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8.
看了如图,在平面直角坐标系中,O为...的网友还看了以下:
把9(a-b)^2+12(a^2-b^2)+4(a+b)^2分解因式为 2020-03-30 …
因式分解,-4x^3+16x^2-26xmn(m-n)-m(n-m)5(x-y)^3+10(y-x 2020-04-08 …
已知一次函数y=(a-2)x+3a^2-12,a为何值时,一次函数的图象经过点(6, 2020-04-26 …
地理昼夜的问题已知日出为A时:昼长=2×(12-A),夜长=2A,A+B=24时已知日落为B时:昼 2020-05-04 …
请大家帮我算几个概率问题,谢谢本人数学比较娖,算不来,大家帮我算算吧.1,有12个数字,每次随机选 2020-06-03 …
已知椭圆x^2+2y^2=12,A是x轴正半轴的一定点已知椭圆x^2+2y^2=12,A是x轴正半 2020-06-29 …
已知实数a,b满足(a*2+b*2)*2+(a*2+b*2)=12,a*2+b*2=?如题 2020-07-30 …
(1)试证明无论x,y为何值,4x^2-12x+9y^2+30y+36的值都为正数.(2)2a^2+ 2020-10-31 …
关于ARM立即数的表示范围?为什么用12bit来表示一个立即数,可以表示的范围为-2^31~2^31 2020-11-07 …
一道数学题已知:直角三角形的周长为20厘米,斜边长为8厘米.求这个三角形的面积我哪里错了?设一直角边 2021-02-07 …