早教吧作业答案频道 -->数学-->
我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.(1)证明“准菱形”性质:“准菱形”的一条对角线平分一个内角.(要求:根据图1写出已知,求证,证明)已
题目详情
我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
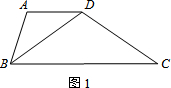
(1)证明“准菱形”性质:“准菱形”的一条对角线平分一个内角.
(要求:根据图1写出已知,求证,证明)
已知:___
求证:___
证明:∵AB=AD,
∴∠ABD=∠BDA,
又∵AD∥BC,
∴∠DBC=∠BDA.
∴∠ABD=∠DBC.
即BD平分∠ABC
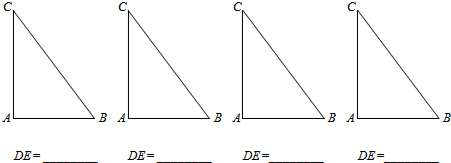
(2)已知,在△ABC中,∠A=90°,AB=3,AC=4.若点D,E分别在边BC,AC上,且四边形ABDE为“准菱形”.请在下列给出的△ABC中(图2),作出满足条件的所有“准菱形”ABDE,并写出相应DE的长.(所给△ABC不一定都用,不够可添)

(1)证明“准菱形”性质:“准菱形”的一条对角线平分一个内角.
(要求:根据图1写出已知,求证,证明)
已知:___
求证:___
证明:∵AB=AD,
∴∠ABD=∠BDA,
又∵AD∥BC,
∴∠DBC=∠BDA.
∴∠ABD=∠DBC.
即BD平分∠ABC
(2)已知,在△ABC中,∠A=90°,AB=3,AC=4.若点D,E分别在边BC,AC上,且四边形ABDE为“准菱形”.请在下列给出的△ABC中(图2),作出满足条件的所有“准菱形”ABDE,并写出相应DE的长.(所给△ABC不一定都用,不够可添)

▼优质解答
答案和解析
(1)已知:如图,“准菱形”ABCD中,AB=AD,AD∥BC,(AD≠BC).
求证:BD平分∠ABC.
证明: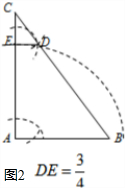
∵AB=AD,
∴∠ABD=∠BDA,
又∵AD∥BC,
∴∠DBC=∠BDA.
∴∠ABD=∠DBC.
即BD平分∠ABC;
故答案为:如图,“准菱形”ABCD中,AB=AD,AD∥BC,(AD≠BC);BD平分∠ABC;∵AB=AD,∴∠ABD=∠BDA,又∵AD∥BC,∴∠DBC=∠BDA.∴∠ABD=∠DBC.即BD平分∠ABC;
(2)可以作出如下四种图形,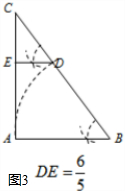
∵∠A=90°,AB=3,AC=4,
∴BC=5,
如图2,当AE=AB,DE∥AB时,
=
,即
=
,
解得,DE=
;
如图3,当BA=BD,DE∥AB时,
=
,即
=
,
解得,DE=
;
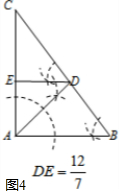
如图4,当EA=ED,DE∥AB时,
=
,即
=
,
解得,DE=
;
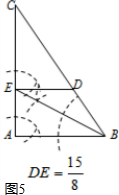
如图5,当DE=BD,DE∥AB时,
=
,即
=
,
解得,DE=
.
求证:BD平分∠ABC.
证明:

∵AB=AD,
∴∠ABD=∠BDA,
又∵AD∥BC,
∴∠DBC=∠BDA.
∴∠ABD=∠DBC.
即BD平分∠ABC;
故答案为:如图,“准菱形”ABCD中,AB=AD,AD∥BC,(AD≠BC);BD平分∠ABC;∵AB=AD,∴∠ABD=∠BDA,又∵AD∥BC,∴∠DBC=∠BDA.∴∠ABD=∠DBC.即BD平分∠ABC;
(2)可以作出如下四种图形,

∵∠A=90°,AB=3,AC=4,
∴BC=5,
如图2,当AE=AB,DE∥AB时,
| DE |
| AB |
| CE |
| CA |
| DE |
| 3 |
| 1 |
| 4 |
解得,DE=
| 3 |
| 4 |
如图3,当BA=BD,DE∥AB时,
| DE |
| AB |
| CD |
| CB |
| DE |
| 3 |
| 2 |
| 5 |
解得,DE=
| 6 |
| 5 |
如图4,当EA=ED,DE∥AB时,
| DE |
| AB |
| CE |
| CA |
| DE |
| 3 |
| 4-DE |
| 4 |

解得,DE=
| 12 |
| 7 |
如图5,当DE=BD,DE∥AB时,
| DE |
| AB |
| CD |
| CB |
| DE |
| 3 |
| 5-DE |
| 5 |

解得,DE=
| 15 |
| 8 |
看了 我们把有一组邻边相等,一组对...的网友还看了以下:
读图,回答问题.(1)按序号写出①-③的简称,④-⑥的行政中心:;(2)图中临海的有,陆上有邻国接 2020-05-17 …
某化工厂排放污水,给附近的相邻居民造成侵害和损失,邻近居民有权请求( )A.停止污染B.精神补偿C. 2020-05-22 …
某化工厂排放污水,给附近的相邻居民造成侵害和损失,邻近居民有权请求( )。A.停止污染B. 2020-05-22 …
几个数学问题,请教一下!1.有邻补角,那有没有邻余角?2.邻补角和对顶角会不会同时出现?也就是说, 2020-06-15 …
邻二氮菲和邻菲啰啉是同一种东西吗?请详细说明.GB6781-2007中引用GB/T603的邻二氮菲 2020-07-06 …
5乘5方格问题有*,%,#,@四种不同的图形在5*5的方格中填入,要求@必须与#,%,*相邻(斜线 2020-07-30 …
18.(2015山东济宁中考)阅读下面的文字,按要求作文。生活在世界上,总会有邻居,人与人、人与动物 2020-11-13 …
(2014•翔安区质检)如果一元二次方程ax2+bx+c=0的两根x1、x2均为正数,且满足1<x1 2020-11-27 …
相邻关系中必要的便利,相邻关系因种类不同而具有不同的内容.但基本上是相邻一方有权要求他方提供必要的便 2020-12-07 …
阅读下面的材料,根据要求写一篇不少于800字的文章。有个人看到邻居家做豆腐非常成功,远近闻名,便也想 2020-12-11 …